Since Minkowski's time, much progress has been made in the geometry of numbers, even as far as the geometry of numbers of convex bodies is concerned. But, surprisingly, one rather obvious interpretation of classical theorems in this theory has so far escaped notice.

Minkowski's basic theorem establishes an upper estimate for the smallest positive value of a convex distance function F(x) on the lattice of all points x with integral coordinates. By contrast, we shall establish a lower estimate for F(x) at all the real points X on a suitable hyperplane

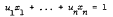
with integral coefficients u1, …, un not all zero. We arrive at this estimate by means of applying to Minkowski's Theorem the classical concept of polarity relative to the unit hypersphere

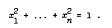
This concept of polarity allows generally to associate with known theorems on point lattices analogous theorems on what we call hyperplane lattices. These new theorems, although implicit in the old ones, seem to have some interest and perhaps further work on hyperplane lattices may lead to useful results.

In the first sections of this note a number of notations and results from the classical theory will be collected. The later sections deal then with the consequences of polarity.