No CrossRef data available.
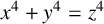 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 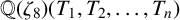 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$Published online by Cambridge University Press: 07 November 2024
Ishitsuka et al. [‘Explicit calculation of the mod 4 Galois representation associated with the Fermat quartic’, Int. J. Number Theory 16(4) (2020), 881–905] found all points on the Fermat quartic 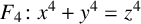 ${F_4\colon x^4+y^4=z^4}$ over quadratic extensions of
${F_4\colon x^4+y^4=z^4}$ over quadratic extensions of 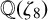 ${\mathbb {Q}}(\zeta _8)$, where
${\mathbb {Q}}(\zeta _8)$, where 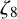 $\zeta _8$ is the eighth primitive root of unity
$\zeta _8$ is the eighth primitive root of unity 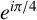 $e^{i\pi /4}$. Using Mordell’s technique, we give an alternative proof for the result of Ishitsuka et al. and extend it to the rational function field
$e^{i\pi /4}$. Using Mordell’s technique, we give an alternative proof for the result of Ishitsuka et al. and extend it to the rational function field 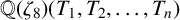 ${\mathbb {Q}}({\zeta _8})(T_1,T_2,\ldots ,T_n)$.
${\mathbb {Q}}({\zeta _8})(T_1,T_2,\ldots ,T_n)$.
The author is supported by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) (grant number 101.04-2023.21).
Dedicated to Professor Andrew Bremner