Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T01:20:04.092Z Has data issue: false hasContentIssue false
  • English
  • Français

PERMUTATION POLYNOMIALS OF DEGREE 8 OVER FINITE FIELDS OF ODD CHARACTERISTIC

Part of: Finite fields and commutative rings (number-theoretic aspects) Computational aspects of field theory and polynomials

Published online by Cambridge University Press:  09 July 2019

XIANG FAN Open the ORCID record for XIANG FAN [Opens in a new window]
XIANG FAN*
Affiliation:
School of Mathematics, Sun Yat-sen University, Guangzhou 510275, China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an algorithmic generalisation of Dickson’s method of classifying permutation polynomials (PPs) of a given degree 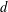$d$ over finite fields. Dickson’s idea is to formulate from Hermite’s criterion several polynomial equations satisfied by the coefficients of an arbitrary PP of degree 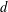$d$. Previous classifications of PPs of degree at most 6 were essentially deduced from manual analysis of these polynomial equations, but this approach is no longer viable for 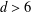$d>6$. Our idea is to calculate some radicals of ideals generated by the polynomials, implemented by a computer algebra system. Our algorithms running in SageMath 8.6 on a personal computer work very fast to determine all PPs of degree 8 over an arbitrary finite field of odd order 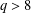$q>8$. Such PPs exist if and only if 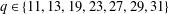$q\in \{11,13,19,23,27,29,31\}$ and are explicitly listed in normalised form.

Keywords

permutation polynomialHermite’s criterionCarlitz conjectureSageMath

MSC classification

Primary: 11T06: Polynomials
Secondary: 12Y05: Computational aspects of field theory and polynomials
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 40 - 55
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by the Natural Science Foundation of Guangdong Province (No. 2018A030310080). The author was also sponsored by the National Natural Science Foundation of China (No. 11801579).

References

Chahal, J. S. and Ghorpade, S. R., ‘Carlitz–Wan conjecture for permutation polynomials and Weil bound for curves over finite fields’, Finite Fields Appl. 54 (2018), 366–375.Google Scholar
Cohen, S. D. and Fried, M. D., ‘Lenstra’s proof of the Carlitz–Wan conjecture on exceptional polynomials: an elementary version’, Finite Fields Appl. 1(3) (1995), 372–375.Google Scholar
Decker, W., Greuel, G.-M., Pfister, G. and Schönemann, H., ‘Singular 4-1-2: A computer algebra system for polynomial computations’, 2019, https://www.singular.uni-kl.de.Google Scholar
Dickson, L. E., ‘The analytic representation of substitutions on a power of a prime number of letters with a discussion of the linear group’, Ann. of Math. (2) 11(1–6) (1896–1897), 65–120.Google Scholar
Ding, C. and Yuan, J., ‘A family of skew Hadamard difference sets’, J. Combin. Theory Ser. A 113(7) (2006), 1526–1535.Google Scholar
Fan, X., ‘The Weil bound and non-exceptional permutation polynomials over finite fields’, Preprint, 2018, arXiv:1811.12631.Google Scholar
Fan, X., ‘A classification of permutation polynomials of degree 7 over finite fields’, Finite Fields Appl. 59 (2019), 1–21.Google Scholar
Fan, X., ‘Permutation polynomials of degree $8$ over finite fields of characteristic $2$ ’, Preprint, 2019, arXiv:1903.10309.Google Scholar
Fried, M. D., Guralnick, R. and Saxl, J., ‘Schur covers and Carlitz’s conjecture’, Israel J. Math. 82(1–3) (1993), 157–225.Google Scholar
Hayes, D. R., ‘A geometric approach to permutation polynomials over a finite field’, Duke Math. J. 34 (1967), 293–305.Google Scholar
Hermite, C., ‘Sur les fonctions de sept lettres’, C. R. Acad. Sci. Paris 57 (1863), 750–757.Google Scholar
Hou, X.-D., ‘Permutation polynomials over finite fields — a survey of recent advances’, Finite Fields Appl. 32 (2015), 82–119.Google Scholar
Kemper, G., ‘The calculation of radical ideals in positive characteristic’, J. Symbolic Comput. 34(3) (2002), 229–238.Google Scholar
Li, J., Chandler, D. B. and Xiang, Q., ‘Permutation polynomials of degree 6 or 7 over finite fields of characteristic 2’, Finite Fields Appl. 16(6) (2010), 406–419.Google Scholar
Lidl, R. and Niederreiter, H., Finite Fields, 2nd edn, Encyclopedia of Mathematics and its Applications, 20 (Cambridge University Press, Cambridge, 1997).Google Scholar
Mullen, G. L. (ed), Handbook of Finite Fields, Discrete Mathematics and its Applications (CRC Press, Boca Raton, FL, 2013).Google Scholar
The Sage Developers, SageMath, the Sage Mathematics Software System, version 8.6, 2019, https://www.sagemath.org.Google Scholar
von zur Gathen, J., ‘Values of polynomials over finite fields’, Bull. Aust. Math. Soc. 43(1) (1991), 141–146.Google Scholar
Wan, D. Q., ‘A p-adic lifting lemma and its applications to permutation polynomials’, in: Finite Fields, Coding Theory, and Advances in Communications and Computing (Las Vegas, NV, 1991), Lecture Notes in Pure and Applied Mathematics, 141 (Dekker, New York, 1993), 209–216.Google Scholar