Published online by Cambridge University Press: 03 July 2019
A Ducci sequence is a sequence of integer  $n$-tuples generated by iterating the map Such a sequence is eventually periodic and we denote by
$n$-tuples generated by iterating the map Such a sequence is eventually periodic and we denote by 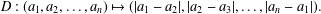 $$\begin{eqnarray}D:(a_{1},a_{2},\ldots ,a_{n})\mapsto (|a_{1}-a_{2}|,|a_{2}-a_{3}|,\ldots ,|a_{n}-a_{1}|).\end{eqnarray}$$
$$\begin{eqnarray}D:(a_{1},a_{2},\ldots ,a_{n})\mapsto (|a_{1}-a_{2}|,|a_{2}-a_{3}|,\ldots ,|a_{n}-a_{1}|).\end{eqnarray}$$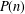 $P(n)$ the maximal period of such sequences for given
$P(n)$ the maximal period of such sequences for given  $n$. We prove a new upper bound in the case where
$n$. We prove a new upper bound in the case where  $n$ is a power of a prime
$n$ is a power of a prime 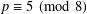 $p\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$ for which
$p\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$ for which 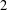 $2$ is a primitive root and the Pellian equation
$2$ is a primitive root and the Pellian equation 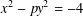 $x^{2}-py^{2}=-4$ has no solutions in odd integers
$x^{2}-py^{2}=-4$ has no solutions in odd integers  $x$ and
$x$ and 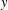 $y$.
$y$.