Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stojaković, Miloš
2003.
Limit shape of optimal convex lattice polygons in the sense of different metrics.
Discrete Mathematics,
Vol. 271,
Issue. 1-3,
p.
235.
Prodromou, Maria N.
2005.
Limit shape of convex lattice polygons with minimal perimeter.
Discrete Mathematics,
Vol. 300,
Issue. 1-3,
p.
139.


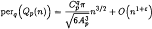 . for arbitrary ɛ > 0,
where
. for arbitrary ɛ > 0,
where
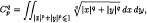 .
and
.
and 