Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T15:04:31.253Z Has data issue: false hasContentIssue false
  • English
  • Français

Path decompositions of digraphs

Published online by Cambridge University Press:  17 April 2009

Issam Abdul-Kader
Issam Abdul-Kader
Affiliation:
Faculty of Science, Lebanese University, Beirut, Lebanon.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G = (X, U) be a digraph of order n. P(G) denotes the minimal cardinal of a path-partition of the arcs of G.

Oystein Ore, Theory of graphs (Amer. Math. Soc, Providence, Rhode Island, 1962) has proved that , where 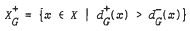. We say that G satisfies Q if the preceeding inequality is an equality.

We give some properties of the digraphs satisfying Q, and in particular the case where G is strongly connected. Then we prove that P(G) ≤ [n2/4], and that this result is the best possible. Next we exhibit the existence of digraphs with circuits such that P(G) = [n2/4].

Finally we prove that if G is a strongly connected digraph of order n which satisfies Q, then there exists a strongly connected digraph H of order n + 1 having G as a sub-digraph and satisfying Q, too.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 19 , Issue 2 , October 1978 , pp. 205 - 216
Copyright
Copyright © Australian Mathematical Society 1979

References

[1]Abdul-Kader, Issam, “Sur des graphes ayant un circuit hamiltonien unique et sur des invariants des cheminements dans les graphes orientés” (Thèses de Doctorat d'Etat lere, Université Pierre et Marie Curie, Paris, 1977).Google Scholar
[2]Abdul-Kader, Issam, “Indice de partition en chemins des arcs des tournois ayant un seul circuit hamiltonien”, Problèmes combinatoires et théorie des graphes, Orsay, Juillet, 1976, 1–2 (Colloques Internationaux du Centre National de la Recherche Scientifique, 260. Centre National de la Recherche Scientifique, Paris, 1978).Google Scholar
[3]Alspach, Brian, Mason, David W., Pullman, Norman J., “Path numbers of tournaments”, preprint.Google Scholar
[4]Alspach, Brian R. and Pullman, Norman J., “Path decompositions of digraphs”, Bull. Austral. Math. Soc. 10 (1974), 421–427.CrossRefGoogle Scholar
[5]Berge, C., Graphes et hypergraphes (Dunod Université, 604. Dunod, Paris, 1970).Google Scholar
[6]Chaty, G. et Chein, M., “Invariants liés aux chemins dans les graphes sans circuits”, Colloquio Internazionale sulle Teorie Combinatorie con la collaborazione della American Mathematical Society, Roma, 1973, Tomo I, 287–308 (Atti dei Convegni Lincei, 17. Academia Nazionale dei Lincei, Roma, 1976).Google Scholar
[7]Chaty, G., Chein, M., “Path-number of k-graphs and symmetric digraphs”, Proceedings of the Seventh Southeastern Conference on Combinatorics, Graph Theory, and Computing, 203–216 (Louisana State University, Baton Rouge, 1976. Congressus Numerantium, 17. Utilitas Mathematica, Winnipeg, 1976).Google Scholar
[8]O'Brien, Richard C., “An upper bound on the path number of a digraph”, J. Combinatorial Theory Ser. B 22 (1977), 168–174.Google Scholar
[9]Ore, Oystein, Theory of graphs (American Mathematical Society Colloquium Publications, 38. American Mathematical Society, Providence, Rhode Island, 1962).Google Scholar