Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T16:54:16.808Z Has data issue: false hasContentIssue false
  • English
  • Français

PARTITIONS OF THE SET OF NONNEGATIVE INTEGERS WITH THE SAME REPRESENTATION FUNCTIONS

Part of: Sequences and sets

Published online by Cambridge University Press:  04 October 2017

JIA-WEN LI  and
MIN TANG
JIA-WEN LI
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China email [email protected]
MIN TANG*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

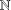Let $\mathbb{N}$ be the set of all nonnegative integers. For a given set 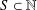$S\subset \mathbb{N}$ the representation function 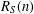$R_{S}(n)$ counts the number of solutions of the equation 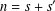$n=s+s^{\prime }$ with 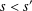$s<s^{\prime }$ and 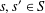$s,s^{\prime }\in S$. We obtain some results on a problem of Chen and Lev [‘Integer sets with identical representation functions’, Integers16 (2016), Article ID A36, 4 pages] about sets 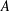$A$ and 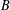$B$ such that 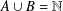$A\cup B=\mathbb{N}$, 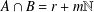$A\cap B=r+m\mathbb{N}$ and whose representation functions coincide.

Keywords

partitionrepresentation function

MSC classification

Primary: 11B34: Representation functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 200 - 206
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by National Natural Science Foundation of China, grant no. 11471017.

References

Chen, Y. G. and Lev, V. F., ‘Integer sets with identical representation functions’, Integers 16 (2016), Article ID A36, 4 pages.Google Scholar
Dombi, G., ‘Additive properties of certain sets’, Acta Arith. 103 (2002), 137–146.CrossRefGoogle Scholar
Kiss, S. Z. and Sándor, C., ‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161.Google Scholar
Kiss, S. Z. and Sándor, C., ‘On the structure of sets which has coinciding representation functions’, Preprint, 2017 arXiv:1702.04499v1.Google Scholar
Lev, V. F., ‘Reconstructing integer sets from their representation functions’, Electron. J. Combin. 11 (2004), Article ID R78.CrossRefGoogle Scholar
Sándor, C., ‘Partitions of natural numbers and their representation functions’, Integers 4 (2004), Article ID A18.Google Scholar
Tang, M., ‘Partitions of the set of natural numbers and their representation functions’, Discrete Math. 308 (2008), 2614–2616.Google Scholar
Tang, M., ‘Partitions of natural numbers and their representation functions’, Chin. Ann. Math. Ser. A 37 (2016), 41–46; English version, Chinese J. Contemp. Math. 37 (2016), 39–44.Google Scholar
Yu, W. and Tang, M., ‘A note on partitions of natural numbers and their representation functions’, Integers 12 (2012), Article ID A53, 5 pages.Google Scholar