No CrossRef data available.
Published online by Cambridge University Press: 14 December 2022
In this paper, we show that every pair of sufficiently large even integers can be represented as a pair of eight prime cubes and k powers of 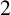 $2$. In particular, we prove that
$2$. In particular, we prove that 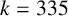 $k=335$ is admissible, which improves the previous result.
$k=335$ is admissible, which improves the previous result.
This work is supported by the National Natural Science Foundation of China (Grant No. 12171286).