Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-12T09:47:05.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation theorems for semilinear hyperbolic and ultrahyperbolic operators

Published online by Cambridge University Press:  17 April 2009

Mamoru Narita
Mamoru Narita
Affiliation:
Department of Mathematics, Faculty of Science, Hiroshima University, Hiroshima, Japan.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The oscillation property of the semilinear hyperbolic or ultra-hyperbolic operator L defined by

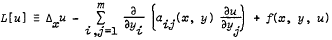
is studied. Sufficient conditions are provided for all solutions of uL[u] ≤ 0 satisfying certain boundary conditions to be oscillatory. The basis of our results is the non-existence of positive solutions of the associated differential inequalities.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 18 , Issue 1 , February 1978 , pp. 55 - 64
Copyright
Copyright © Australian Mathematical Society 1978

References

[1]Kahane, Charles, “Oscillation theorems for solutions of hyperbolic equations”, Proc. Amer. Math. Soc. 41 (1973), 183–188.CrossRefGoogle Scholar
[2]Kreith, Kurt, “Sturmian theorems for hyperbolic equations”, Proc. Amer. Math. Soc. 22 (1969), 277–281.Google Scholar
[3]Kreith, Kurt, “Sturmian theorems for characteristic initial value problems”, Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 47 (1969), 139–144.Google Scholar
[4]Naito, Manabu and Yoshida, Norio, “Oscillation theorems for semilinear elliptic differential operators”, submitted.Google Scholar
[5]Narita, Mamoru and Yoshida, Norio, “Oscillation theorems for linear ultrahyperbolic operators”, submitted.Google Scholar
[6]Noussair, E.S. and Swanson, C.A., “Oscillation theory for semilinear Schrödinger equations and inequalities”, Proc. Roy. Soc. Edinburgh Sect. A 75 (1975–1976), 67–81.Google Scholar
[7]Pagan, Gordon, “Oscillation theorems for characteristic initial value problems for linear hyperbolic equations”, Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 55 (1973), 301–313.Google Scholar
[8]Travis, C.C., “Comparison and oscillation theorems for hyperbolic equations”, Utilitas Math. 6 (1974), 139–151.Google Scholar
[9]Young, Eutiquio C., “Comparison and oscillation theorems for singular hyperbolic equations”, Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 59 (1975), 383–391.Google Scholar