Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-29T14:28:06.886Z Has data issue: false hasContentIssue false
  • English
  • Français

OPERATORS ON C0(L,X) WHOSE RANGE DOES NOT CONTAIN c0

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  01 June 2008

JARNO TALPONEN
JARNO TALPONEN*
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, Box 68, Gustaf Hällströminkatu 2b, FI-00014 Helsinki, Finland (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper contains two results: (a) if 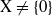is a Banach space and (L,τ) is a nonempty locally compact Hausdorff space without isolated points, then each linear operator T:C0(L,X)→C0(L,X) whose range does not contain an isomorphic copy of c00 satisfies the Daugavet equality 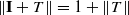; (b) if Γ is a nonempty set and X and Y are Banach spaces such that X is reflexive and Y does not contain c0 isomorphically, then any continuous linear operator T:c0(Γ,X)→Y is weakly compact.

Keywords

Daugavet equationweakly compact operatorsvector-valued function spaces

MSC classification

Secondary: 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 77 , Issue 3 , June 2008 , pp. 515 - 520
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Bombal, F. and Cembranos, P., ‘The Dieudonné property of C(K,E)’, Trans. Amer. Math. Soc. 285 (1984), 649–656.Google Scholar
[2]Cembranos, P., ‘C(K,E) contains a complemented copy of c 0’, Proc. Amer. Math. Soc. 91 (1984), 556–558.Google Scholar
[3]Diestel, J. and Uhl, J. Jr, Vector Measures, Mathematical Surveys, 15 (American Mathematical Society, Providence, RI, 1977).CrossRefGoogle Scholar
[4]Habala, P., Hajek, P. and Zizler, V., Introduction to Banach Spaces I–II (MatfyzPress, Prague, 1996).Google Scholar
[5]Werner, D., ‘Recent progress on the Daugavet property’, Irish Math. Soc. Bull. 46 (2001), 77–97.CrossRefGoogle Scholar
[6]Willard, S., General Topology (Dover, New York, 2004).Google Scholar