No CrossRef data available.
Published online by Cambridge University Press: 17 April 2009
The statement 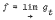 used in proving Theorem 2 of [1] needs explanation. This was pointed out to us by Professor S. Raghwan of Tata Institute of Fundamental Research, Bombay, and we gave the explanation of this in [2]. For the sake of completeness we give here the full proof of the theorem; filling the gap in the proof. We use the same notations and definitions as those of [1]. Also for simplicity of notation we write kmn, gmn and amn to mean km,n, gm,n and a respectively. We need the following lemma.
used in proving Theorem 2 of [1] needs explanation. This was pointed out to us by Professor S. Raghwan of Tata Institute of Fundamental Research, Bombay, and we gave the explanation of this in [2]. For the sake of completeness we give here the full proof of the theorem; filling the gap in the proof. We use the same notations and definitions as those of [1]. Also for simplicity of notation we write kmn, gmn and amn to mean km,n, gm,n and a respectively. We need the following lemma.