Let S be a semigroup contained in a locally compact Abelian group G. Let Ĝ denote the Bohr compactification of G. We say that a sequence 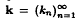contained in S is Hartman uniform distributed on G if

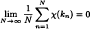
for any character χ in Ĝ. Suppose that (Tg)g∈s is a semigroup of measurable measure preserving transformations of a probability space (X, β, μ) and B is an element of the σ-algebra β of positive μ measure. For a map T: X → X and a set A ⊆ X let T−1A denote {x ∈ X: Tx ∈ A}. In an earlier paper, the author showed that if k is Hartman uniform distributed then

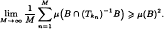
In this paper we show that ≥ cannot be replaced by =. A more detailed discussion of this situation ensues.