No CrossRef data available.
Article contents
ON THE WARING–GOLDBACH PROBLEM FOR ONE SQUARE, FOUR CUBES AND ONE BIQUADRATE
Published online by Cambridge University Press: 15 September 2022
Abstract
Let N be a sufficiently large integer. We prove that, with at most
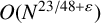 $O(N^{23/48+\varepsilon })$
exceptions, all even positive integers up to N can be represented in the form
$O(N^{23/48+\varepsilon })$
exceptions, all even positive integers up to N can be represented in the form
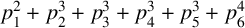 $p_1^2+p_2^3+p_3^3+p_4^3+p_5^3+p_6^4$
, where
$p_1^2+p_2^3+p_3^3+p_4^3+p_5^3+p_6^4$
, where
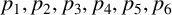 $p_1,p_2,p_3,p_4,p_5,p_6$
are prime numbers.
$p_1,p_2,p_3,p_4,p_5,p_6$
are prime numbers.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work is supported by the National Natural Science Foundation of China (Grant Nos. 11901566, 12001047, 11971476 and 12071238) and the Fundamental Research Funds for the Central Universities (Grant No. 2022YQLX05).



