Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T02:41:14.315Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE PROBABILITY OF GENERATING NILPOTENT SUBGROUPS IN A FINITE GROUP

Part of: Probabilistic methods in group theory Representation theory of groups

Published online by Cambridge University Press:  20 November 2015

S. M. JAFARIAN AMIRI ,
H. MADADI  and
H. ROSTAMI
S. M. JAFARIAN AMIRI*
Affiliation:
Department of Mathematics, Faculty of Sciences, University of Zanjan, PO Box 45371-38791, Zanjan, Iran email [email protected]
H. MADADI
Affiliation:
Department of Mathematics, Faculty of Sciences, University of Zanjan, PO Box 45371-38791, Zanjan, Iran email [email protected]
H. ROSTAMI
Affiliation:
Department of Mathematics, Faculty of Sciences, University of Zanjan, PO Box 45371-38791, Zanjan, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 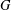$G$ be a finite group. We denote by 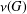${\it\nu}(G)$ the probability that two randomly chosen elements of 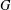$G$ generate a nilpotent subgroup and by 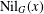$\text{Nil}_{G}(x)$ the set of elements 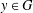$y\in G$ such that 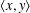$\langle x,y\rangle$ is a nilpotent subgroup. A group 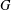$G$ is called an 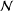${\mathcal{N}}$-group if 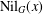$\text{Nil}_{G}(x)$ is a subgroup of 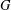$G$ for all 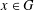$x\in G$. We prove that if 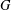$G$ is an 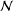${\mathcal{N}}$-group with 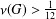${\it\nu}(G)>\frac{1}{12}$, then 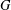$G$ is soluble. Also, we classify semisimple 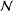${\mathcal{N}}$-groups with 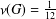${\it\nu}(G)=\frac{1}{12}$.

Keywords

nilpotent groupprobabilityN-group

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 20P05: Probabilistic methods in group theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 3 , June 2016 , pp. 447 - 453
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abdollahi, A. and Zarrin, M., ‘Non-nilpotent graph of a group’, Comm. Algebra 38(12) (2010), 4390–4403.CrossRefGoogle Scholar
Blyth, R. D. and Robinson, D. J. S., ‘Semisimple groups with the rewritting property Q 5’, Comm. Algebra 23(6) (1995), 2171–2180.Google Scholar
Dubose-Schmidt, R., Galloy, M. D. and Wilson, D. L., Counting nilpotent pairs in finite groups: some conjectures, Rose-Hulman Technical Report MS TR 92-05. (1992).Google Scholar
Erdős, P. and Turàn, P., ‘On some problems of statistical group-theory IV’, Acta Math. Acad. Sci. Hungar. 19 (1968), 413–435.Google Scholar
Fulman, J. E., Galloy, M. D., Sherman, G. J. and Vanderkam, J. M., ‘Counting nilpotent pairs in finite groups’, Ars Combin. 54 (2000), 161–178.Google Scholar
The GAP Group, GAP-Groups, Algorithms and Programming, version 4.4.10, 2007, (http://www.gap-system.org).Google Scholar
Guralnick, R. M. and Robinson, G. R., ‘On the commuting probability in finite groups’, J. Algebra 300(2) (2006), 509–528.Google Scholar
Guralnick, R. M. and Wilson, J. S., ‘The probability of generating a finite soluble group’, Proc. Lond. Math. Soc. (3) 81(2) (2000), 405–427.Google Scholar
Gustafson, W. H., ‘What is the probability that two group elements commute?’, Amer. Math. Monthly 80(9) (1973), 1031–1034.Google Scholar
Huppert, B., Endlich Gruppen III (Springer, Berlin, 1982).Google Scholar
Robinson, D. J. S., A Course in the Theory of Groups (Springer, New York, 1996).Google Scholar
Thompson, J. G., ‘Nonsolvable finite groups all of whose local subgroups are solvable’, Bull. Amer. Math. Soc. 74(3) (1968), 383–437.Google Scholar