Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T12:05:44.088Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE PRIME GRAPH OF SIMPLE GROUPS

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  08 October 2014

TIMOTHY C. BURNESS  and
ELISA COVATO
TIMOTHY C. BURNESS*
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK email [email protected]
ELISA COVATO
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 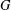$G$ be a finite group, let 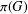${\it\pi}(G)$ be the set of prime divisors of 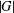$|G|$ and let 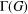${\rm\Gamma}(G)$ be the prime graph of $G$. This graph has vertex set 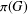${\it\pi}(G)$, and two vertices $r$ and $s$ are adjacent if and only if 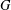$G$ contains an element of order $rs$. Many properties of these graphs have been studied in recent years, with a particular focus on the prime graphs of finite simple groups. In this note, we determine the pairs 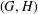$(G,H)$, where 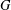$G$ is simple and 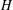$H$ is a proper subgroup of 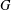$G$ such that 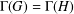${\rm\Gamma}(G)={\rm\Gamma}(H)$.

Keywords

finite simple groupsprime graphsmaximal subgroups

MSC classification

Primary: 20E32: Simple groups
Secondary: 20E28: Maximal subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 227 - 240
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aschbacher, M. and Seitz, G. M., ‘Involutions in Chevalley groups over fields of even order’, Nagoya Math. J. 63 (1976), 1–91.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: The user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Burness, T. C., ‘Fixed point ratios in actions of finite classical groups, II’, J. Algebra 309 (2007), 80–138.CrossRefGoogle Scholar
Burness, T. C. and Giudici, M., Classical Groups, Derangements and Primes, Australian Mathematical Society Lecture Series (Cambridge University Press, Cambridge) , to appear.CrossRefGoogle Scholar
Covato, E., ‘On boundedly generated subgroups of profinite groups’, J. Algebra 406 (2014), 20–45.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups, Number 3, American Mathematical Society Monographs and Surveys Series, 40 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Hagie, M., ‘The prime graph of a sporadic simple group’, Comm. Algebra 31 (2003), 4405–4424.CrossRefGoogle Scholar
Khosravi, B., ‘On the prime graph of a finite group’, in: Groups St Andrews (Bath, 2009), Vol. 2, London Mathematical Society Lecture Note Series, 388 (Cambridge University Press, Cambridge, 2011), 424–428.CrossRefGoogle Scholar
Kleidman, P. B. and Liebeck, M. W., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Kondrat’ev, A. S., ‘On prime graph components of finite simple groups’, Math. USSR-Sb. 67 (1990), 235–247.Google Scholar
Kondrat’ev, A. S. and Mazurov, V. D., ‘Recognition of alternating groups of prime degree from the orders of their elements’, Sib. Math. J. 41 (2000), 294–302.Google Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., ‘Transitive subgroups of primitive permutation groups’, J. Algebra 234 (2000), 291–361.Google Scholar
Liebeck, M. W. and Seitz, G. M., Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras, American Mathematical Society Monographs and Surveys Series, 180 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Lucchini, A., Morigi, M. and Shumyatsky, P., ‘Boundedly generated subgroups of finite groups’, Forum Math. 24 (2012), 875–887.CrossRefGoogle Scholar
Wall, G. E., ‘On the conjugacy classes in the unitary, symplectic and orthogonal groups’, J. Aust. Math. Soc. 3 (1963), 1–62.Google Scholar
Williams, J. S., ‘Prime graph components of finite groups’, J. Algebra 69 (1981), 487–513.Google Scholar
Zavarnitsine, A. V., ‘On the recognition of finite groups by the prime graph’, Algebra Logic 45 (2006), 220–231.Google Scholar
Zsigmondy, K., ‘Zur Theorie der Potenzreste’, Monatsh. Math. Phys. 3 (1892), 265–284.CrossRefGoogle Scholar
Zvezdina, M. A., ‘On nonabelian simple groups with the same prime graph as an alternating group’, Sib. Math. J. 54 (2013), 47–55.Google Scholar