No CrossRef data available.
Article contents
ON THE PARITY OF THE GENERALISED FROBENIUS PARTITION FUNCTIONS 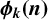 $\boldsymbol {\phi _k(n)}$
$\boldsymbol {\phi _k(n)}$
Published online by Cambridge University Press: 15 June 2022
Abstract
Andrews [Generalized Frobenius Partitions, Memoirs of the American Mathematical Society, 301 (American Mathematical Society, Providence, RI, 1984)] defined two families of functions,
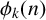 $\phi _k(n)$
and
$\phi _k(n)$
and
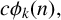 $c\phi _k(n),$
enumerating two types of combinatorial objects which he called generalised Frobenius partitions. Andrews proved a number of Ramanujan-like congruences satisfied by specific functions within these two families. Numerous other authors proved similar results for these functions, often with a view towards a specific choice of the parameter
$c\phi _k(n),$
enumerating two types of combinatorial objects which he called generalised Frobenius partitions. Andrews proved a number of Ramanujan-like congruences satisfied by specific functions within these two families. Numerous other authors proved similar results for these functions, often with a view towards a specific choice of the parameter
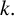 $k.$
Our goal is to identify an infinite family of values of k such that
$k.$
Our goal is to identify an infinite family of values of k such that
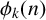 $\phi _k(n)$
is even for all n in a specific arithmetic progression; in particular, we prove that, for all positive integers
$\phi _k(n)$
is even for all n in a specific arithmetic progression; in particular, we prove that, for all positive integers
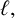 $\ell ,$
all primes
$\ell ,$
all primes
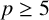 $p\geq 5$
and all values
$p\geq 5$
and all values
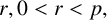 $r, 0 < r < p,$
such that
$r, 0 < r < p,$
such that
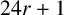 $24r+1$
is a quadratic nonresidue modulo
$24r+1$
is a quadratic nonresidue modulo
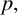 $p,$
$p,$
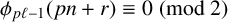 $$ \begin{align*} \phi_{p\ell-1}(pn+r) \equiv 0 \pmod{2} \end{align*} $$
$$ \begin{align*} \phi_{p\ell-1}(pn+r) \equiv 0 \pmod{2} \end{align*} $$
for all
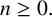 $n\geq 0.$
Our proof of this result is truly elementary, relying on a lemma from Andrews’ memoir, classical q-series results and elementary generating function manipulations. Such a result, which holds for infinitely many values of
$n\geq 0.$
Our proof of this result is truly elementary, relying on a lemma from Andrews’ memoir, classical q-series results and elementary generating function manipulations. Such a result, which holds for infinitely many values of
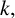 $k,$
is rare in the study of arithmetic properties satisfied by generalised Frobenius partitions, primarily because of the unwieldy nature of the generating functions in question.
$k,$
is rare in the study of arithmetic properties satisfied by generalised Frobenius partitions, primarily because of the unwieldy nature of the generating functions in question.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 431 - 436
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was partially supported by Simons Foundation Grant 633284.



