No CrossRef data available.
Published online by Cambridge University Press: 27 February 2023
For any real polynomial 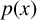 $p(x)$ of even degree k, Shapiro [‘Problems around polynomials: the good, the bad and the ugly
$p(x)$ of even degree k, Shapiro [‘Problems around polynomials: the good, the bad and the ugly $\ldots $’, Arnold Math. J. 1(1) (2015), 91–99] proposed the conjecture that the sum of the number of real zeros of the two polynomials
$\ldots $’, Arnold Math. J. 1(1) (2015), 91–99] proposed the conjecture that the sum of the number of real zeros of the two polynomials 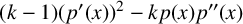 $(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)$ and
$(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)$ and 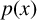 $p(x)$ is larger than 0. We prove that the conjecture is true except in one case: when the polynomial
$p(x)$ is larger than 0. We prove that the conjecture is true except in one case: when the polynomial 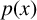 $p(x)$ has no real zeros, the derivative polynomial
$p(x)$ has no real zeros, the derivative polynomial 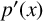 $p{'}(x)$ has one real simple zero, that is,
$p{'}(x)$ has one real simple zero, that is, 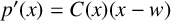 $p{'}(x)=C(x)(x-w)$, where
$p{'}(x)=C(x)(x-w)$, where 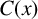 $C(x)$ is a polynomial with
$C(x)$ is a polynomial with 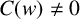 $C(w)\ne 0$, and the polynomial
$C(w)\ne 0$, and the polynomial 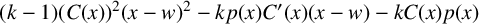 $(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$ has no real zeros.
$(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$ has no real zeros.