Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
BLIZNAC, MARIJA
and
FILIPIN, ALAN
2016.
AN UPPER BOUND FOR THE NUMBER OF DIOPHANTINE QUINTUPLES.
Bulletin of the Australian Mathematical Society,
Vol. 94,
Issue. 3,
p.
384.
Lapkova, Kostadinka
2017.
On the average number of divisors of reducible quadratic polynomials.
Journal of Number Theory,
Vol. 180,
Issue. ,
p.
710.
Lapkova, Kostadinka
2018.
Explicit upper bound for the average number of divisors of irreducible quadratic polynomials.
Monatshefte für Mathematik,
Vol. 186,
Issue. 4,
p.
663.
DUDEK, ADRIAN W.
PAŃKOWSKI, ŁUKASZ
and
SCHARASCHKIN, VICTOR
2019.
NOTE ON THE NUMBER OF DIVISORS OF REDUCIBLE QUADRATIC POLYNOMIALS.
Bulletin of the Australian Mathematical Society,
Vol. 99,
Issue. 1,
p.
1.
Ye, Dongxi
2020.
Revisiting the average number of divisors of a quadratic polynomial.
Monatshefte für Mathematik,
Vol. 192,
Issue. 2,
p.
465.
Ye, Dongxi
2021.
A remark on the average number of divisors of a quadratic polynomial.
Archiv der Mathematik,
Vol. 116,
Issue. 1,
p.
49.
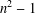 $n^{2}-1$
$n^{2}-1$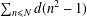 $\sum _{n\leq N}d(n^{2}-1)$, where
$\sum _{n\leq N}d(n^{2}-1)$, where 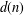 $d(n)$ denotes the number of divisors of
$d(n)$ denotes the number of divisors of  $n$. During the course of our proof, we also furnish an asymptotic formula for the sum
$n$. During the course of our proof, we also furnish an asymptotic formula for the sum 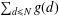 $\sum _{d\leq N}g(d)$, where
$\sum _{d\leq N}g(d)$, where 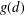 $g(d)$ denotes the number of solutions
$g(d)$ denotes the number of solutions  $x$ in
$x$ in 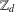 $\mathbb{Z}_{d}$ to the equation
$\mathbb{Z}_{d}$ to the equation 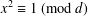 $x^{2}\equiv 1~(\text{mod}~d)$.
$x^{2}\equiv 1~(\text{mod}~d)$.