Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fulman, Jason
2001.
Random matrix theory over finite fields.
Bulletin of the American Mathematical Society,
Vol. 39,
Issue. 1,
p.
51.
Vera-López, A.
Arregi, J. M.
Ormaetxea, Leyre
Vera-López, F. J.
and
Basova, Olga
2016.
Equalities on the number of conjugacy classes of the Sylow p-subgroups of GL(n, q).
Israel Journal of Mathematics,
Vol. 214,
Issue. 2,
p.
675.


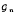 the group of the upper unitriangular matrices over
the group of the upper unitriangular matrices over 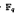 , the finite field with
, the finite field with 