Let 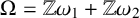$\Omega =\mathbb {Z}\omega _1+\mathbb {Z}\omega _2$ be a lattice in $\mathbb {C}$ with invariants 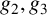$g_2,g_3$ and 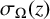$\sigma _{\Omega }(z)$ the associated Weierstrass 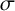$\sigma $-function. Let 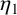$\eta _1$ and 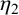$\eta _2$ be the quasi-periods associated to 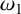$\omega _1$ and 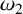$\omega _2$, respectively. Assuming 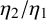$\eta _2/\eta _1$ is a nonzero real number, we give an upper bound for the number of algebraic points on the graph of 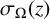$\sigma _{\Omega }(z)$ of bounded degrees and bounded absolute Weil heights in some unbounded region of $\mathbb {C}$ in the following three cases: (i) 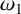$\omega _1$ and 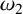$\omega _2$ algebraic; (ii) 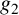$g_2$ and 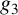$g_3$ algebraic; (iii) the algebraic points are far from the lattice points.