Hostname: page-component-599cfd5f84-96rnj Total loading time: 0 Render date: 2025-01-07T07:00:32.350Z Has data issue: false hasContentIssue false
  • English
  • Français

On the norming constants occuring in convergent Markov chains

Published online by Cambridge University Press:  17 April 2009

Harry Cohn
Harry Cohn
Affiliation:
Department of Statistics, Institute of Advanced Studies, Australian National University, Canberra, Act.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

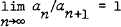Several theorems concerning the norming constants {aṇ} and {bn} making a normed Markov chain {an (Xn+bn): n ≥ 0} convergent in distribution (or in probability) are given. It is shown that if Rényi's mixing conditions holds, and 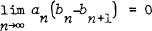, whereas in the general case 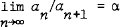with α ≠ 0 and 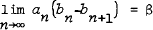exists and are finite. Examples regarding maxima of independent and identically distributed random variables, random walk, and branching processes are considered.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 17 , Issue 2 , October 1977 , pp. 193 - 205
Copyright
Copyright © Australian Mathematical Society 1977

References

[1]Darling, D.A., “The Galton-Watson process with infinite mean”, J. Appl. Probability 7 (1970), 455–456.CrossRefGoogle Scholar
[2]Hewitt, Edwin and Savage, Leonard J., “Symmetric measures on cartesian products”, Trans. Amer. Math. Soc. 80 (1955), 470–501.CrossRefGoogle Scholar
[3]Heyde, C.C., “Extension of a result of Seneta for the supercritical Galton Watson process”, Ann. Math. Statist. 41 (1970), 739–742.CrossRefGoogle Scholar
[4]Loève, Michel, Probability theory, third edition (Van Nostrand, Princeton, New Jersey; Toronto; New York; London; 1963).Google Scholar
[5]Orey, Steven, Lecture notes on limit theorems for Markov chain transition probabilities (Van Nostrand Reinhold, London, New York, Cincinnati, Toronto, Melbourne, 1971).Google Scholar
[6]Rényi, A., “On mixing sequences of sets”, Acta Math. Acad. Sci. Hungar. 9 (1958), 215–228.CrossRefGoogle Scholar
[7]Rényi, A. and Révész, P., “On mixing sequences of random variables”, Acta Math. Acad. Sci. Hungar. 9 (1958), 389–393.CrossRefGoogle Scholar
[8]Richter, W., “Zu einigen Konvergenzeigenschaften von Folgen zufälliger Elemente”, Studia Math. 25 (1965), 231–243.CrossRefGoogle Scholar
[9]Richter, Wolfgang, “Das Null-Eins-Gesetz und ein Grenzwertsatz für zufällige Prozesse mit diskreter zufälliger Zeit”, Wiss. Z. Techn. Univ. Dresden 14 (1965), 497–504.Google Scholar
[10]Seneta, E., “On recent theorems concerning the supercritical Galton-Watson process”, Ann. Math. Statist. 39 (1968), 2098–2102.CrossRefGoogle Scholar
[11]Seneta, E., “The simple branching process with infinite mean. I”, J. Appl. Probability 10 (1973), 206–212.Google Scholar