Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T11:49:55.352Z Has data issue: false hasContentIssue false
  • English
  • Français

On the normal version of the simplicial cohomology of operator algebras

Published online by Cambridge University Press:  17 April 2009

A.Ya. Helemskii  and
Z.A. Lykova
A.Ya. Helemskii
Affiliation:
Chair of function Theory and Functional Analysis Faculty of Mechanics and Mathematics, Moscow State University, Moscow 119899GSP, Russia
Z.A. Lykova
Affiliation:
Chair of Algebra and Analysis, Moscow Institute of Electronic Machine, Industry B.Vuzovskii 3/12 Moscow 109028, Russia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the normal version 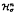(R, R.) of the Banach simplicial cohomology of operator algebras can be expressed in terms of the functor Ext on the category of Banach R-bimodules. As an application, we prove that 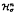(R, R*) = Hn(R, R*) and thus the latter space vanishes for some von Heumann algebras for positive τ.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 48 , Issue 3 , December 1993 , pp. 407 - 410
Copyright
Copyright © Australian Mathematical Society 1993

References

[1]Christensen, E. and Sinclair, A.M., ‘On the vanishing of H n(A, A*) for certain C*-algebras’, Pacific J. Math. 137 (1989), 55–63.Google Scholar
[2]Haagerup, U., ‘All nuclear C*-algebras are amenable’, Invent. Math. 73 (1983), 305–319.CrossRefGoogle Scholar
[3]Helemskii, A.Ya., ‘The homological essence of Connes amenability: injectivity of the predual bimodule’, (in Russian), Mat. Sb. 180 (1989), 1680–1690. Math. USSR Sbornik 68 (1991), 555–566.Google Scholar
[4]Helemskii, A.Ya., The Homology in Banach and topological algebras, (in Russian) (Moscow Univ. Press, Moscow, 1986). (Kluwer Academic Publishers, Dordrecht, 1989) (in English).CrossRefGoogle Scholar
[5]Helemskii, A.Ya., ‘Expression of the normal cohomology in terms of “Ext”, and some applications’, Math. Nachr. 145 (1990), 55–58.CrossRefGoogle Scholar
[6]Johnson, B.E., Kadison, R.V. and Ringrose, J.R., ‘Cohomology of operator algebras, III’, Bull. Soc. Math. France 100 (1972), 73–96.CrossRefGoogle Scholar