No CrossRef data available.
Published online by Cambridge University Press: 22 October 2024
Let  $\zeta _K(s)$ denote the Dedekind zeta-function associated to a number field K. We give an effective upper bound for the height of the first nontrivial zero other than
$\zeta _K(s)$ denote the Dedekind zeta-function associated to a number field K. We give an effective upper bound for the height of the first nontrivial zero other than 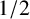 $1/2$ of
$1/2$ of  $\zeta _K(s)$ under the generalised Riemann hypothesis. This is a refinement of the earlier bound obtained by Sami [‘Majoration du premier zéro de la fonction zêta de Dedekind’, Acta Arith. 99(1) (2000), 61–65].
$\zeta _K(s)$ under the generalised Riemann hypothesis. This is a refinement of the earlier bound obtained by Sami [‘Majoration du premier zéro de la fonction zêta de Dedekind’, Acta Arith. 99(1) (2000), 61–65].