Published online by Cambridge University Press: 02 December 2022
We extend a result of Lieb [‘On the lowest eigenvalue of the Laplacian for the intersection of two domains’, Invent. Math. 74(3) (1983), 441–448] to the fractional setting. We prove that if A and B are two bounded domains in 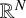 $\mathbb R^N$ and
$\mathbb R^N$ and 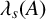 $\lambda _s(A)$,
$\lambda _s(A)$, 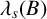 $\lambda _s(B)$ are the lowest eigenvalues of
$\lambda _s(B)$ are the lowest eigenvalues of 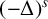 $(-\Delta )^s$,
$(-\Delta )^s$,  $0<s<1$, with Dirichlet boundary conditions, there exists some translation
$0<s<1$, with Dirichlet boundary conditions, there exists some translation 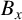 $B_x$ of B such that
$B_x$ of B such that  $\lambda _s(A\cap B_x)< \lambda _s(A)+\lambda _s(B)$. Moreover, without the boundedness assumption on A and B, we show that for any
$\lambda _s(A\cap B_x)< \lambda _s(A)+\lambda _s(B)$. Moreover, without the boundedness assumption on A and B, we show that for any 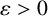 $\varepsilon>0$, there exists some translation
$\varepsilon>0$, there exists some translation 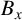 $B_x$ of B such that
$B_x$ of B such that 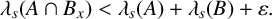 $\lambda _s(A\cap B_x)< \lambda _s(A)+\lambda _s(B)+\varepsilon .$
$\lambda _s(A\cap B_x)< \lambda _s(A)+\lambda _s(B)+\varepsilon .$