Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-10T23:12:20.435Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE LND CONJECTURE

Part of: Affine geometry Differential algebra

Published online by Cambridge University Press:  03 July 2023

XIAOSONG SUN  and
BEINI WANG
XIAOSONG SUN*
Affiliation:
School of Mathematical Sciences, Jilin University, Changchun, Jilin 130012, PR China
BEINI WANG
Affiliation:
School of Mathematical Sciences, Jilin University, Changchun, Jilin 130012, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let k be a field of characteristic zero and 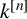$k^{[n]}$ the polynomial algebra in n variables over k. The LND conjecture concerning the images of locally nilpotent derivations arose from the Jacobian conjecture. We give a positive answer to the LND conjecture in several cases. More precisely, we prove that the images of rank-one locally nilpotent derivations of 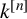$k^{[n]}$ acting on principal ideals are MZ-subspaces for any 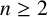$n\geq 2$, and that the images of a large class of locally nilpotent derivations of 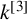$k^{[3]}$ (including all rank-two and homogeneous rank-three locally nilpotent derivations) acting on principal ideals are MZ-subspaces.

Keywords

locally nilpotent derivationsJacobian conjectureLND conjectureMZ-subspaces

MSC classification

Primary: 14R15: Jacobian problem
Secondary: 13N15: Derivations 14R10: Affine spaces (automorphisms, embeddings, exotic structures, cancellation problem)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 412 - 421
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the EDJPC (JJKH20220962KJ), NSFJP (20210101469JC) and NSFC (12171194).

References

Bass, H., Connel, E. and Wright, D., ‘The Jacobian conjecture: reduction of degree and formal expansion of the inverse’, Bull. Amer. Math. Soc. (N.S.) 7 (1982), 287–330.10.1090/S0273-0979-1982-15032-7CrossRefGoogle Scholar
Cohn, P. M., ‘Bezout rings and their subrings’, Math. Proc. Cambridge Philos. Soc. 64(2) (1968), 251–264.10.1017/S0305004100042791CrossRefGoogle Scholar
Françoise, J. P., Pakovich, F., Yomdin, Y. and Zhao, W. H., ‘Moment vanishing problem and positivity: some examples’, Bull. Sci. Math. 135 (2011), 10–32.10.1016/j.bulsci.2010.06.002CrossRefGoogle Scholar
Freudenburg, G., Algebraic Theory of Locally Nilpotent Derivations, 2nd edn, Invariant Theory and Algebraic Transformation Groups, 7, Encyclopaedia of Mathematical Sciences, 136 (Springer, Berlin, 2017).10.1007/978-3-662-55350-3CrossRefGoogle Scholar
Gilmer, R., Commutative Semigroup Rings (University of Chicago Press, Chicago, IL, 1984).Google Scholar
Liu, D. and Sun, X., ‘The factorial conjecture and images of locally nilpotent derivations’, Bull. Aust. Math. Soc. 101(1) (2020), 71–79.10.1017/S0004972719000546CrossRefGoogle Scholar
Liu, D., Sun, X. and Zeng, X., ‘Images of locally nilpotent derivations acting on ideals of polynomial algebras’, Publ. Math. Debrecen, to appear.Google Scholar
Mathieu, O., ‘Some conjectures about invariant theory and their applications’, in: Algèbre Non Commutative, Groupes Quantiques et Invariants, Reims, 1995 (eds. J. Alev and G. Cauchon), Sémin. Congr., 2 (Soc. Math. France, Paris, 1997), 263–279.Google Scholar
Sun, X., ‘Images of derivations of polynomial algebras with divergence zero’, J. Algebra 492 (2017), 414–418.10.1016/j.jalgebra.2017.09.020CrossRefGoogle Scholar
Sun, X. and Liu, D., ‘Images of locally nilpotent derivations of polynomial algebras in three variables’, J. Algebra 569 (2021), 401–415.10.1016/j.jalgebra.2020.10.025CrossRefGoogle Scholar
van den Essen, A., Polynomial Automorphisms and the Jacobian Conjecture, Progress in Mathematics, 190 (Birkhäuser, Basel–Boston–Berlin, 2000).10.1007/978-3-0348-8440-2CrossRefGoogle Scholar
van den Essen, A., ‘An introduction to Mathieu subspaces’, Preprint, 2019, arXiv:1907.06107.Google Scholar
van den Essen, A. and Sun, X., ‘Monomial preserving derivations and Mathieu–Zhao subspaces’, J. Pure Appl. Algebra 222 (2018), 3219–3223.10.1016/j.jpaa.2017.12.003CrossRefGoogle Scholar
van den Essen, A., Willems, R. and Zhao, W., ‘Some results on the vanishing conjecture of differential operators with constant coefficients’, J. Pure Appl. Algebra 219(9) (2015), 3847–3861.10.1016/j.jpaa.2014.12.024CrossRefGoogle Scholar
van den Essen, A., Wright, D. and Zhao, W., ‘Images of locally finite derivations of polynomial algebras in two variables’, J. Pure Appl. Algebra 215(9) (2011), 2130–2134.10.1016/j.jpaa.2010.12.002CrossRefGoogle Scholar
van den Essen, A., Wright, D. and Zhao, W., ‘On the image conjecture’, J. Algebra 340(1) (2011), 211–224.10.1016/j.jalgebra.2011.04.036CrossRefGoogle Scholar
Zhao, W., ‘Images of commuting differential operators of order one with constant leading coefficients’, J. Algebra 324 (2010), 231–247.10.1016/j.jalgebra.2010.04.022CrossRefGoogle Scholar
Zhao, W., ‘Generalization of the images conjecture and the Mathieu conjecture’, J. Pure Appl. Algebra 214(7) (2010), 1200–1216.10.1016/j.jpaa.2009.10.007CrossRefGoogle Scholar
Zhao, W., ‘Mathieu subspaces of associative algebras’, J. Algebra 350(1) (2012), 245–272.10.1016/j.jalgebra.2011.09.036CrossRefGoogle Scholar
Zhao, W., ‘Some open problems on locally finite or locally nilpotent derivations and $\varepsilon$ -derivations’, Commun. Contemp. Math. 20(4) (2018), Article no. 1750056.10.1142/S0219199717500560CrossRefGoogle Scholar