Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T10:52:52.056Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE GROWTH OF LINEAR RECURRENCES IN FUNCTION FIELDS

Part of: Diophantine approximation, transcendental number theory Sequences and sets Algebraic number theory: global fields

Published online by Cambridge University Press:  09 November 2020

CLEMENS FUCHS Open the ORCID record for CLEMENS FUCHS [Opens in a new window]  and
SEBASTIAN HEINTZE Open the ORCID record for SEBASTIAN HEINTZE [Opens in a new window]
CLEMENS FUCHS*
Affiliation:
Department of Mathematics, University of Salzburg, Hellbrunnerstr. 34, A-5020Salzburg, Austria
SEBASTIAN HEINTZE
Affiliation:
Department of Mathematics, University of Salzburg, Hellbrunnerstr. 34, A-5020Salzburg, Austria e-mail: [email protected]
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 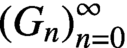$ (G_n)_{n=0}^{\infty } $ be a nondegenerate linear recurrence sequence whose power sum representation is given by 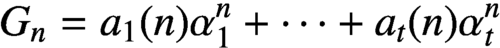$ G_n = a_1(n) \alpha _1^n + \cdots + a_t(n) \alpha _t^n $ . We prove a function field analogue of the well-known result in the number field case that, under some nonrestrictive conditions, 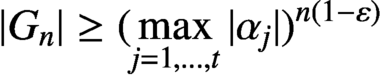$ |{G_n}| \geq ( \max _{j=1,\ldots ,t} |{\alpha _j}| )^{n(1-\varepsilon )} $ for 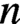$ n $ large enough.

Keywords

function fieldslinear recurrencesS-units

MSC classification

Primary: 11B37: Recurrences
Secondary: 11J87: Schmidt Subspace Theorem and applications 11R58: Arithmetic theory of algebraic function fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 11 - 20
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

Supported by Austrian Science Fund (FWF): I4406.

References

Akiyama, S., Evertse, J.-H. and Pethő, A., ‘On nearly linear recurrence sequences’ (English summary), in: Number Theory – Diophantine Problems, Uniform Distribution and Applications (Springer, Cham, 2017), 1–24.Google Scholar
Bugeaud, Y. and Kaneko, H., ‘On perfect powers in linear recurrence sequences of integers’, Kyushu J. Math. 73 (2019), 221–227.CrossRefGoogle Scholar
Evertse, J.-H., ‘On sums of $S$ -units and linear recurrences’, Comp. Math. 53(2) (1984), 225–244.Google Scholar
Fuchs, C. and Heintze, S., ‘Perfect powers in polynomial power sums’, Preprint, 2019, arXiv:1912.10033.Google Scholar
Fuchs, C., Karolus, C. and Kreso, D., ‘Decomposable polynomials in second order linear recurrence sequences’, Manuscripta Math. 159(3) (2019), 321–346.CrossRefGoogle Scholar
Fuchs, C. and Pethő, A., ‘Effective bounds for the zeros of linear recurrences in function fields’, J. Théor. Nombres Bordeaux 17 (2005), 749–766.CrossRefGoogle Scholar
Mason, R. C., Diophantine Equations over Function Fields, London Mathematical Society Lecture Notes, 96 (Cambridge University Press, Cambridge, 1984).CrossRefGoogle Scholar
van der Poorten, A. J., ‘Some problems of recurrent interest’, Topics in Classical Number Theory, Vol. I, II (Budapest, 1981), Colloquia Mathematica Societatis Janos Bolyai, 34 (North-Holland, Amsterdam, 1984), 1265–1294.Google Scholar
van der Poorten, A. J., ‘Some facts that should be better known, especially about rational functions’, Number Theory and Applications (Kluwer Academic, Dordrecht, 1989), 497–528.Google Scholar
van der Poorten, A. J. and Schlickewei, H. P., ‘The growth conditions for recurrence sequences’, Macquarie Mathematical Reports 82-0041 (1982) (Macquarie University, Sydney, 2019).Google Scholar
van der Poorten, A. J. and Shparlinski, I., ‘On sequences of polynomials defined by certain recurrence relations’, Acta Sci. Math. (Szeged) 61 (1995), 77–103.Google Scholar
Schmidt, W. M., ‘The zero multiplicity of linear recurrence sequences’, Acta Math. 182 (1999), 243–282.CrossRefGoogle Scholar
Stichtenoth, H., Algebraic Function Fields and Codes, Universitext (Springer, Berlin, 1993).Google Scholar
Zannier, U., ‘On composite lacunary polynomials and the proof of a conjecture of Schinzel’, Invent. Math. 174(1) (2008), 127–138.CrossRefGoogle Scholar