Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T10:59:09.606Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EXPONENTIAL DIOPHANTINE EQUATION x2+p2m=2yn

Part of: Diophantine equations

Published online by Cambridge University Press:  21 February 2012

HUILIN ZHU ,
MAOHUA LE  and
ALAIN TOGBÉ
HUILIN ZHU*
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, PR China (email: [email protected])
MAOHUA LE
Affiliation:
Department of Mathematics, Zhanjiang Normal College, Zhanjiang 524048, PR China (email: [email protected])
ALAIN TOGBÉ
Affiliation:
Department of Mathematics, Purdue University North Central, 1401 S. U.S. 421, Westville, IN 46391, USA (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be an odd prime. In this paper, we consider the equation 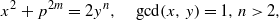and we describe all its solutions. Moreover, we prove that this equation has no solution (x,y,m,n) when n>3 is an odd prime and y is not the sum of two consecutive squares. This extends the work of Tengely [On the diophantine equation x2+q2m=2yp, Acta Arith.127(1) (2007), 71–86].

Keywords

exponential Diophantine equationLehmer numberprimitive divisor

MSC classification

Secondary: 11D61: Exponential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 86 , Issue 2 , October 2012 , pp. 303 - 314
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2012

Footnotes

The first author was partly supported by the Fundamental Research Funds for the Central Universities (No. 2011121039). The second author was supported by the National Science Foundation of China (No. 10971184). The third author was supported by Purdue University North Central.

References

[1]Abu Muriefah, F. S., Luca, F., Siksek, S. and Tengely, S., ‘On the diophantine equation x 2+C=2y n’, Int. J. Number Theory 5(6) (2009), 1117–1128.CrossRefGoogle Scholar
[2]Bennett, M. A. and Skinner, C. M., ‘Ternary diophantine equations via Galois representations and modular forms’, Canad. J. Math. 56(1) (2004), 23–54.CrossRefGoogle Scholar
[3]Bilu, Y., Hanrot, G. and Voutier, F. M., ‘Existence of primitive divisors of Lucas and Lehmer numbers (with an appendix by M. Mignotte)’, J. reine angew. Math. 539 (2001), 75–122.Google Scholar
[4]Wieb, B., John, C. and Catherine, P., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.Google Scholar
[5]Bugeaud, Y. and Shorey, T. N., ‘On the number of solutions of the generalized Ramanujan–Nagell equation’, J. reine angew. Math. 539 (2001), 55–74.Google Scholar
[6]Daberkow, M., Fieker, C., Kluners, J., Pohst, M. E., Roegner, K. and Wildanger, K., ‘Kant V4’, J. Symbolic Comput. 24 (1997), 267–283.CrossRefGoogle Scholar
[7]Ke, Z., ‘On the diophantine equation x 2=y n+1, xy≠0’, Sci. Sinica 14(5) (1964), 457–460.Google Scholar
[8]Lebesgue, V. A., ‘Sur l’impossibilité, en nombres entiers, de l’équation x m=y 2+1’, Nouv. Ann. Math. 9(1) (1850), 178–181.Google Scholar
[9]Ljunggren, W., ‘Zur theorie der Gleichung x 2+1=Dy 4’, Det Norske Vid.-Akad. Avh. I. 5 (1942), 27.Google Scholar
[10]Ljunggren, W., ‘On the diophantine equation Cx 2+D=2y n’, Math. Scand. 18 (1966), 69–86.CrossRefGoogle Scholar
[11]Mordell, L. J., Diophantine Equations (Academic Press, London, 1969).Google Scholar
[12]Petr, K., ‘Sur l’équation de Pell’, C̆asopis Pest. Mat. Fys. 56 (1927), 57–66 (in Czech).CrossRefGoogle Scholar
[13]Pink, I., ‘On the diophantine equation x 2+(p z 11⋅⋅⋅p z nn)2=2y n’, Publ. Math. Debrecen 65(1–2) (2004), 205–213.CrossRefGoogle Scholar
[14]Pink, I. and Tengely, S., ‘Full powers in arithmetic progressions’, Publ. Math. Debrecen 57(3–4) (2000), 535–545.CrossRefGoogle Scholar
[15]Ribenboim, P., ‘The Fibonacci numbers and the Arctic Ocean’, in: Symposia Gaussiana Conf. A (Walter de Gruyter, Berlin, 1995), pp. 41–83.CrossRefGoogle Scholar
[16]Störmer, C., ‘L’équation ’, Bull. Soc. Math. France 27 (1899), 160–170.CrossRefGoogle Scholar
[17]Tengely, S., ‘On the diophantine equation x 2+a 2=2y n’, Indag. Math. (N.S.) 15(2) (2004), 291–304.CrossRefGoogle Scholar
[18]Tengely, S., ‘On the diophantine equation x 2+q 2m=2y p’, Acta Arith. 127(1) (2007), 71–86.CrossRefGoogle Scholar
[19]Voutier, P. M., ‘Primitive divisors of Lucas and Lehmer sequences’, Math. Comp. 64 (1995), 869–888.CrossRefGoogle Scholar
[20]Yuan, P.-Z., ‘On the diophantine equation ax 2+by 2=ck n’, Indag. Math. (N.S.) 16(2) (2005), 301–320.CrossRefGoogle Scholar