Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T22:48:28.602Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ESCAPING SET OF MEROMORPHIC FUNCTIONS WITH DIRECT TRACTS

Part of: Series expansions Entire and meromorphic functions, and related topics Complex dynamical systems Differential equations in the complex domain

Published online by Cambridge University Press:  02 April 2015

ZUXING XUAN  and
JIANHUA ZHENG
ZUXING XUAN*
Affiliation:
Beijing Key Laboratory of Information Service Engineering, Institute of Applied Sciences, Department of General Education, Beijing Union University, Beijing 100101, PR China email [email protected], [email protected]
JIANHUA ZHENG
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 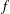$f$ be a transcendental meromorphic function with at least one direct tract. In this note, we investigate the structure of the escaping set which is in the same direct tract. We also give a theorem about the slow escaping set.

Keywords

meromorphic functiondirect tractescaping set

MSC classification

Primary: 30B20: Random power series
Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions 30D10: Representations of entire functions by series and integrals 34M05: Entire and meromorphic solutions 37F10: Polynomials; rational maps; entire and meromorphic functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 1 , August 2015 , pp. 68 - 76
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bergweiler, W., ‘The size of Wiman–Valiron disks’, Complex Var. Elliptic Equ. 56 (2011), 13–33.CrossRefGoogle Scholar
Bergweiler, W., Rippon, P. J. and Stallard, G. M., ‘Dynamics of meromorphic functions with direct or logarithmic singularities’, Proc. Lond. Math. Soc. (3) 97(3) (2008), 368–400.CrossRefGoogle Scholar
Domínguez, P., ‘Dynamics of transcendental meromorphic functions’, Ann. Acad. Sci. Fenn. Math. 23(1) (1998), 225–250.Google Scholar
Eremenko, A. E., ‘On the iteration of entire functions’, in: Dynamical Systems and Ergodic Theory, Banach Center Publications, 23 (Polish Scientific, Warsaw, 1989), 339–345.Google Scholar
Mueller, C. and Rudin, W., ‘Proper holomorphic maps of plane regions’, Complex Var. Theory Appl. 17(1–2) (1991), 113–121.Google Scholar
Rippon, P. J. and Stallard, G. M., ‘Escaping points of meromorphic functions with a finite number of poles’, J. Anal. Math. 96 (2005), 225–245.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M., ‘Dimensions of Julia sets of meromorphic functions with a finite number of poles’, Ergodic Theory Dynam. Systems 26(2) (2006), 525–538.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M., ‘Singularities of meromorphic functions with Baker domains’, Math. Proc. Cambridge Philos. Soc. 141(2) (2006), 371–382.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M., ‘On multiply connected wandering domains of meromorphic functions’, J. Lond. Math. Soc. (2) 77(2) (2008), 405–423.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M., ‘Slow escaping points of meromorphic functions’, Trans. Amer. Math. Soc. 363(8) (2011), 4171–4201.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M., ‘Fast escaping points of entire functions’, Proc. Lond. Math. Soc. (3) 105(3) (2012), 787–820.CrossRefGoogle Scholar
Schleicher, D., ‘Dynamics of entire functions’, Lecture Notes in Math. 1998 (2010), 295–339.CrossRefGoogle Scholar
Selberg, H. L., ‘Eine Ungleichung der Potentialtheorie und ihre Anwendung in der Theorie der meromorphen Funktionen’, Comment. Math. Helv. 18 (1946), 309–326.CrossRefGoogle Scholar
Teichmüller, O., ‘Eine Umkehrung des zweiten Hauptsatzes der Wertverteilungstheorie’, Deutsche Math. 2 (1937), 96–107.Google Scholar
Zheng, J. H., ‘On uniformly perfect boundary of stable domains in iteration of meromorphic functions II’, Math. Proc. Cambridge Philos. Soc. 132(3) (2002), 531–544.Google Scholar
Zheng, J. H., ‘On multiply-connected Fatou components in iteration of meromorphic functions’, J. Math. Anal. Appl. 313(1) (2006), 24–37.CrossRefGoogle Scholar
Zheng, J. H., ‘On fixed-points and singular values of transcendental meromorphic functions’, Sci. China Math. 53(3) (2010), 887–894.CrossRefGoogle Scholar