Let (X, S) be a measurable space and S be a σ-algebra of subsets of X. A nonempty class M is said to be a class of null sets if M ⊂ S, M is closed under countable unions of sets and E ∩ F ∈ M whenever E ∈ M and F ∈ S. It is possible to show that such concepts as absolute continuity, singularity and independence of measures can be studied simply by classes of null sets and that similar results can be obtained under the condition that each disjoint subclass of S – M is countable, denoted (S – M)C. If (X, S,μ) is a measure space then M = {E ∈ S: μ(E) = O} is a class of null sets of S and S – M the class of all sets of positive measure. We say that a measure μ has the property σ if there exists a sequence of totally finite measures 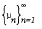on S such that σ(E) = 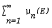for all E ∈ S. This property of measures is weaker than total σ–finiteness of measures. The main result of the present paper is as follows: Let (X, S,μ) be a measure space and M = {E ∈ S: μ(E) = O}. Then (S – M)C if and only if μ has the property σ.