Published online by Cambridge University Press: 16 February 2012
Let 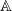 be a commutative algebraic group defined over a number field K. For a prime ℘ in K where
be a commutative algebraic group defined over a number field K. For a prime ℘ in K where 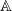 has good reduction, let N℘,n be the number of n-torsion points of the reduction of
has good reduction, let N℘,n be the number of n-torsion points of the reduction of 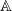 modulo ℘ where n is a positive integer. When
modulo ℘ where n is a positive integer. When 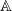 is of dimension one and n is relatively prime to a fixed finite set of primes depending on
is of dimension one and n is relatively prime to a fixed finite set of primes depending on 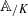 , we determine the average values of N℘,n as the prime ℘ varies. This average value as a function of n always agrees with a divisor function.
, we determine the average values of N℘,n as the prime ℘ varies. This average value as a function of n always agrees with a divisor function.
Research partially supported by National Science Council, Republic of China.