Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T04:12:02.960Z Has data issue: false hasContentIssue false
  • English
  • Français

On the differential equation for the conventional tide-well system

Published online by Cambridge University Press:  17 April 2009

B.J. Noye
B.J. Noye
Affiliation:
Department of Applied Mathematics, University of Adelaide, Adelaide, South Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper discusses solutions to the differential equation

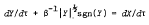
which governs the height

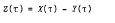
of the non-dimensional water level inside a conventional tide-well when the corresponding height of the sea-level outside is X(τ). A perturbation solution correct to O(β4), for small β, for the particular case X = sinτ described previously has been extended to O(β6) for any function X(τ) differentiable at least three times. Two special cases, where X(τ) is a single sinusoid and the sum of two sinusoids, are treated in detail.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 7 , Issue 2 , October 1972 , pp. 251 - 267
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Brown, A., “On the differential equations for tide-well systems” Bull. Austral. Math. Soc. 5 (1971), 175–185.CrossRefGoogle Scholar
[2]Noye, B.J., “The frequency response of a tide-well”. Proc. 3rd Austral. Conf. on Hydraulics and Fluid Mechanics, Sydney, 1968, 65–71.Google Scholar
[3]Noye, B.J., “On a class of differential equations which model tide-well systems” Bull. Austral. Math. Soc. 3 (1970), 391–411.CrossRefGoogle Scholar
[4]Rossiter, J.R. and Lennon, G.W., “An intensive analysis of shallow water tides” Geophys. J.R. Astron. Soc. 16 (1968), 275–293.CrossRefGoogle Scholar
[5]Zetler, B.D. and Cummings, R.A., “A harmonic method for predicting shallow-water tides” J. Marine Res. 25 (1967), 103–114.Google Scholar