Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tirao, Paulo
2001.
On the homology of graded Lie algebras.
Journal of Pure and Applied Algebra,
Vol. 156,
Issue. 2-3,
p.
357.
Pouseele, Hannes
and
Tirao, Paulo
2005.
Constructing Lie algebra homology classes.
Journal of Algebra,
Vol. 292,
Issue. 2,
p.
585.
Pouseele, Hannes
2005.
On the cohomology of extensions by a Heisenberg Lie algebra.
Bulletin of the Australian Mathematical Society,
Vol. 71,
Issue. 3,
p.
459.
Fialowski, Alice
and
Millionschikov, Dmitri
2006.
Cohomology of graded Lie algebras of maximal class.
Journal of Algebra,
Vol. 296,
Issue. 1,
p.
157.
Pouseele, Hannes
2007.
Betti Number Behavior for Nilpotent Lie Algebras.
Geometriae Dedicata,
Vol. 122,
Issue. 1,
p.
77.
Tillyer, Rob
Engel, Robin S.
and
Wooldredge, John
2008.
The intersection of racial profiling research and the law.
Journal of Criminal Justice,
Vol. 36,
Issue. 2,
p.
138.
Luo, Li
2009.
Cohomology of Oriented Tree Diagram Lie Algebras.
Communications in Algebra,
Vol. 37,
Issue. 3,
p.
965.
Cagliero, Leandro
and
Tirao, Paulo
2014.
The cohomology of filiform Lie algebras of maximal rank.
Linear Algebra and its Applications,
Vol. 455,
Issue. ,
p.
143.
Khaksari, Ahmad
2015.
Betti number of nilpotent Lie algebras and graph ideals.
Asian-European Journal of Mathematics,
Vol. 08,
Issue. 03,
p.
1550046.
Yang, Yong
and
Liu, Wende
2018.
On cohomology of filiform Lie superalgebras.
Journal of Geometry and Physics,
Vol. 134,
Issue. ,
p.
212.
Alvarez, María Alejandra
and
Rosales-Gómez, Javier
2020.
Cohomology of Lie Superalgebras.
Symmetry,
Vol. 12,
Issue. 5,
p.
833.
Alvarez, María Alejandra
2020.
The Betti numbers for Heisenberg Lie algebras.
Journal of Algebraic Combinatorics,
Vol. 52,
Issue. 4,
p.
461.


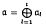 induced by
induced by 