Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fomenko, O. M.
1980.
Applications of the theory of modular forms to number theory.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 4,
p.
1307.
Mahler, K
1982.
Fifty years as a mathematician.
Journal of Number Theory,
Vol. 14,
Issue. 2,
p.
121.
Cohen, Paula
1984.
On the coefficients of the transformation polynomials for the elliptic modular function.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 95,
Issue. 03,
p.
389.
Faisant, Alain
and
Philibert, Georges
1987.
Quelques résultats de transcendance liés à l'invariant modulaire j.
Journal of Number Theory,
Vol. 25,
Issue. 2,
p.
184.
Diaz, Guy
and
Philibert, Georges
1989.
Growth properties of the modular function j.
Journal of Mathematical Analysis and Applications,
Vol. 139,
Issue. 2,
p.
382.
Bae, Sunghan
and
Lee, Seungjae
1997.
On the Coefficients of the Drinfeld Modular Equation.
Journal of Number Theory,
Vol. 66,
Issue. 1,
p.
85.
Hsia, Liang-chung
1998.
On the Coefficients of Modular Polynomials for Drinfeld Modules.
Journal of Number Theory,
Vol. 72,
Issue. 2,
p.
236.
Charles, Denis
and
Lauter, Kristin
2005.
Computing Modular Polynomials.
LMS Journal of Computation and Mathematics,
Vol. 8,
Issue. ,
p.
195.
Waldschmidt, Michel
2008.
Surveys in Number Theory.
Vol. 17,
Issue. ,
p.
1.
Мироков, Василий Дмитриевич
and
Mirokov, Vasilij Dmitrievich
2009.
О некоторых свойствах модулярного многочлена для лямбда-функции.
Математические заметки,
Vol. 86,
Issue. 2,
p.
237.
Mirokov, V. D.
2009.
On some properties of modular polynomials for the lambda function.
Mathematical Notes,
Vol. 86,
Issue. 1-2,
p.
216.
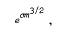 where c > 0 is an absolute constant which can be determined effectively. It seems probable that also in the general case an upper bound of the form
eO(m10gm)
should hold, but I have not so far succeeded in proving such a result.
where c > 0 is an absolute constant which can be determined effectively. It seems probable that also in the general case an upper bound of the form
eO(m10gm)
should hold, but I have not so far succeeded in proving such a result.