Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-31T09:10:26.051Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE BURES METRIC, $C^*$-NORM AND QUANTUM METRIC

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  27 January 2025

KONRAD AGUILAR Open the ORCID record for KONRAD AGUILAR [Opens in a new window] ,
KARINA BEHERA ,
TRON OMLAND  and
NICOLE WU
KONRAD AGUILAR*
Affiliation:
Department of Mathematics and Statistics, Pomona College, 610 N. College Ave., Claremont, CA 91711, USA
KARINA BEHERA
Affiliation:
Department of Mathematics and Statistics, Pomona College, 610 N. College Ave., Claremont, CA 91711, USA e-mail: [email protected]
TRON OMLAND
Affiliation:
Norwegian National Security Authority (NSM) and Department of Mathematics, University of Oslo, Norway e-mail: [email protected]
NICOLE WU
Affiliation:
Department of Mathematics, Harvey Mudd College, 320 E. Foothill Blvd., Claremont, CA 91711, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a unital 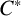$C^*$-algebra and a faithful trace, we prove that the topology on the associated density space induced by the $C^*$-norm is finer than the Bures metric topology. We also provide an example when this containment is strict. 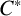Next, we provide a metric on the density space induced by a quantum metric in the sense of Rieffel and prove that the induced topology is the same as the topology induced by the Bures metric and $C^*$-norm when the $C^*$-algebra is assumed to be finite dimensional. Finally, we provide an example where the Bures metric and induced quantum metric are not metric equivalent. Thus, we provide a bridge between these aspects of quantum information theory and noncommutative metric geometry.

Keywords

quantum metric spacesBures metric

MSC classification

Primary: 46L52: Noncommutative function spaces
Secondary: 46L85: Noncommutative topology 81P15: Quantum measurement theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is partially supported by the first author’s NSF grant DMS-2316892.

References

Aguilar, K. and Yu, J., ‘The Fell topology and the modular Gromov–Hausdorff propinquity’, Proc. Amer. Math. Soc. 152(4) (2024), 1711–1724.Google Scholar
Bures, D., ‘An extension of Kakutani’s theorem on infinite product measures to the tensor product of semifinite ${w}^{\ast }$ -algebras’, Trans. Amer. Math. Soc. 135 (1969), 199–212.Google Scholar
Davidson, K. R., ${C}^{\ast }$ -algebras by Example, Fields Institute Monographs, 6 (American Mathematical Society, Providence, RI, 1996).Google Scholar
Farenick, D. and Rahaman, M., ‘Bures contractive channels on operator algebras’, New York J. Math. 23 (2017), 1369–1393.Google Scholar
Farsi, C., Latrémolière, F. and Packer, J., ‘Convergence of inductive sequences of spectral triples for the spectral propinquity’, Adv. Math. 437 (2024), Article no. 109442, 59 pages.CrossRefGoogle Scholar
Hayashi, M., Quantum Information Theory: Mathematical Foundation, 2nd edn, Graduate Texts in Physics (Springer-Verlag, Berlin, 2017).CrossRefGoogle Scholar
Kaad, J. and Kyed, D., ‘Dynamics of compact quantum metric spaces’, Ergodic Theory Dynam. Systems 41(7) (2021), 2069–2109.CrossRefGoogle Scholar
Latrémolière, F., The covariant Gromov–Hausdorff propinquity’, Studia Math. 251(2) (2020), 135–169.CrossRefGoogle Scholar
Latrémolière, F. and Packer, J., ‘Noncommutative solenoids and the Gromov–Hausdorff propinquity’, Proc. Amer. Math. Soc. 145(5) (2017), 2043–2057.CrossRefGoogle Scholar
Reiffel, M. A., ‘Gromov–Hausdorff distance for quantum metric spaces. Matrix algebras converge to the sphere for quantum Gromov–Hausdorff distance’, Mem. Amer. Math. Soc. 168(796) (2004), 67–91.Google Scholar
Rieffel, M. A., ‘Metrics on states from actions of compact groups’, Doc. Math. 3 (1998), 215–229.CrossRefGoogle Scholar