Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Minfeng
Gao, Zongsheng
and
Zhang, Jilong
2018.
Brück Conjecture with Hyper-Order $$\varvec{\sigma }_{{\mathbf {2}}}{\varvec{(}\mathbf {f}\varvec{)}} {\varvec{<}} {\mathbf {1}}$$ σ 2 ( f ) < 1 and Linear Differential Polynomials.
Results in Mathematics,
Vol. 73,
Issue. 4,
Zhang, Guowei
2018.
Infinite growth of solutions of second order complex differential equation.
Open Mathematics,
Vol. 16,
Issue. 1,
p.
1233.
Dam, Arup
and
Majumder, Sujoy
2020.
A power of a combination of meromorphic function with its shift sharing small function with its derivative.
Quaestiones Mathematicae,
Vol. 43,
Issue. 4,
p.
449.
Lahiri, Indrajit
and
Majumder, Sujoy
2020.
A power of a meromorphic function sharing a small function IM with its first derivative.
Bollettino dell'Unione Matematica Italiana,
Vol. 13,
Issue. 1,
p.
113.
Majumder, Sujoy
and
Sarkar, Jeet
2020.
Meromorphic function sharing entire functions IM with its first derivative.
Quaestiones Mathematicae,
Vol. 43,
Issue. 12,
p.
1663.
Majumder, Sujoy
and
Sarkar, Jeet
2022.
On an open problem of Zhang and Yang.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 71,
Issue. 1,
p.
429.
Majumder, Sujoy
and
Dam, Arup
2022.
On an open problem of Lü, Li and Yang.
Filomat,
Vol. 36,
Issue. 11,
p.
3625.
Majumder, Sujoy
and
Sarkar, Rudra Kanta
2023.
Power of Entire Function Sharing Non-zero Polynomials with It’s Linear Differential Polynomial.
Computational Methods and Function Theory,
Vol. 23,
Issue. 1,
p.
23.
Dida, Riad
and
El Farissi, Abdallah
2024.
Brück’s Conjecture for Solutions of Second-Order Complex ODE.
Mediterranean Journal of Mathematics,
Vol. 21,
Issue. 3,
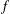 $f$ with hyper-order
$f$ with hyper-order 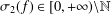 ${\it\sigma}_{2}(f)\in [0,+\infty )\setminus \mathbb{N}$ shares one finite value
${\it\sigma}_{2}(f)\in [0,+\infty )\setminus \mathbb{N}$ shares one finite value  $a$ (counting multiplicities) with its derivative
$a$ (counting multiplicities) with its derivative 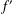 $f^{\prime }$, then
$f^{\prime }$, then 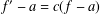 $f^{\prime }-a=c(f-a)$, where
$f^{\prime }-a=c(f-a)$, where  $c$ is a nonzero constant. The conjecture has been established for entire functions with order
$c$ is a nonzero constant. The conjecture has been established for entire functions with order 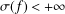 ${\it\sigma}(f)<+\infty$ and hyper-order
${\it\sigma}(f)<+\infty$ and hyper-order 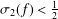 ${\it\sigma}_{2}(f)<{\textstyle \frac{1}{2}}$. The purpose of this paper is to prove the Brück conjecture for the case
${\it\sigma}_{2}(f)<{\textstyle \frac{1}{2}}$. The purpose of this paper is to prove the Brück conjecture for the case 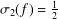 ${\it\sigma}_{2}(f)=\frac{1}{2}$ by studying the infinite hyper-order solutions of the linear differential equations
${\it\sigma}_{2}(f)=\frac{1}{2}$ by studying the infinite hyper-order solutions of the linear differential equations 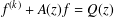 $f^{(k)}+A(z)f=Q(z)$. The shared value
$f^{(k)}+A(z)f=Q(z)$. The shared value  $a$ is extended to be a ‘small’ function with respect to the entire function
$a$ is extended to be a ‘small’ function with respect to the entire function 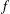 $f$.
$f$.