Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-10T16:47:01.295Z Has data issue: false hasContentIssue false
  • English
  • Français

On the boundary behaviour of Bloch and normal functions

Published online by Cambridge University Press:  17 April 2009

Rauno Aulaskari
Rauno Aulaskari
Affiliation:
Department of Mathematics, University of Joensuu, P.O. Box 111, SF-80101 Joensuu 10, Finland.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Criteria for an analytic function f defined in |z| < 1 to belong to B0, the class of Bloch functions satisfying 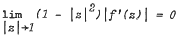, and criteria for a meromorphic function g defined in |z| < 1 to belong to N0, namely, to satisfy 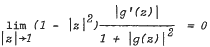are obtained in terms of the area and the length of the images of hyperbolic disks and hyperbolic circles, respectively.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 30 , Issue 2 , October 1984 , pp. 299 - 305
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Dufresnoy, J., “Sur l'aire sphérique décrite par les valeurs d'une fonction méromorphe”. Bull. Sci. Math. 65 (1941), 214–219.Google Scholar
[2]Lappan, P., “A non-normal locally uniformly univalent function”, Bull. London Math. Soc. 5 (1973), 291–294.CrossRefGoogle Scholar
[3]Lehto, O. and Virtanen, K. I., “Boundary behaviour and normal meromorphic functions”, Acta Math. 97 (1957), 47–65.CrossRefGoogle Scholar
[4]Yamashita, S., “Criteria for functions to be Bloch”, Bull. Austral. Math. Soc. 21 (1980), 223–229.CrossRefGoogle Scholar
[5]Yamashita, S., “Functions of uniformly bounded characteristic”. Ann. Acad. Sci. Fenn. Ser. A I Math. 7 (1982), 349–367.Google Scholar