Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T09:15:20.879Z Has data issue: false hasContentIssue false
  • English
  • Français

On the average distance property in finite dimensional real Banach spaces

Published online by Cambridge University Press:  17 April 2009

Reinhard Wolf
Reinhard Wolf
Affiliation:
Institute fur MathematikUniversitat SalzburgHellbrunneratrasse 34 A-5020 Salzburg, Austria
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The average distance Theorem of Gross implies that for each N-dimensional real Banach space E (N ≥ 2) there is a unique positive real number r(E) with the following property: for each positive integer n and for all (not necessarily distinct) x1, x2, …, xn, in E with ‖x1‖ = ‖x2‖ = … = ‖xn‖ = 1, there exists an x in E with ‖x‖ = 1 such that

.

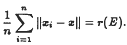In this paper we prove that if E has a 1-unconditional basis then r(E)≤2−(l/N) and equality holds if and only if E is isometrically isomorphic to Rn equipped with the usual 1-norm.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 51 , Issue 1 , February 1995 , pp. 87 - 101
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Clearly, J., Morris, S.A. and Yost, D., ‘Numerical geometry-numbers for shapes’, Amer. Math. Monthly 93 (1986), 260–275.CrossRefGoogle Scholar
[2]Gross, O., ‘The rendezvous value of a metric space’, in Advances in game theory, Annals of Math. Studies 52 (Princeton, 1964), pp. 49–53.Google Scholar
[3]Morric, S.A. and Nickolas, P., ‘On the average distance property of compact connected metric spaces’, Arch. Math. 40 (1983), 459–463.CrossRefGoogle Scholar
[4]Wolf, R., ‘On the average distance property of spheres in Banach spaces’, Arch. Math. 62 (1994), 378–384.CrossRefGoogle Scholar