Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2025-01-03T18:59:55.979Z Has data issue: false hasContentIssue false
  • English
  • Français

On Stieltjes-Volterra integral equations

Published online by Cambridge University Press:  17 April 2009

S.G. Pandit
S.G. Pandit
Affiliation:
Department of Mathematics, Centre of Post-Graduate Instruction and Research, University of Bombay, Panaji, Goa, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Stieltjes-Volterra integral equation system

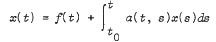
is firstly considered. Pointwise estimates and boundedness of its solutions are obtained under various conditions on the function K. To do this, the well-known Gronwall-Bellman integral inequality is generalized. For a particular choice of u, it is shown that the integral equation reduces to a difference equation. The problem of existence (and non-existence), uniqueness (and non-uniqueness) of the difference equation is discussed. Gronwall-Bellman inequality is further generalized to n linear terms and is subsequently applied to obtain sufficient conditions in order that a certain stability of the unperturbed Volterra system

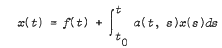
implies the corresponding local stability of the (discontinuously) perturbed system

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 18 , Issue 3 , June 1978 , pp. 321 - 334
Copyright
Copyright © Australian Mathematical Society 1978

References

[1]Bellman, Richard E. and Cooke, Kenneth L., Differential-difference equations (Academic Press, New York, London, 1963).Google Scholar
[2]Corduneanu, Constantin, Integral equations and stability of feedback systems (Mathematics in Science and Engineering, 104. Academic Press [Harcourt Brace Jovanovich], New York and London, 1973).Google Scholar
[3]Das, P.C. and Sharma, R.R., “Existence and stability of measure differential equations”, Czechoslovak Math. J. 22 (97) (1972), 145–158.Google Scholar
[4]Dhongade, U.D. and Deo, S.G., “Pointwise estimates of solutions of some Volterra integral equations”, J. Math. Anal. Appl. 45 (1974), 615–628.CrossRefGoogle Scholar
[5]Jones, G. Stephen, “Fundamental inequalities for discrete and discontinuous functional equations”, J. Soc. Indust. Appl. Math. 12 (1964), 43–57.CrossRefGoogle Scholar
[6]Miller, R.K., Nohel, J.A., and Wong, J.S.W., “Perturbations of Volterra integral equations”, J. Math. Anal. Appl. 25 (1969), 676–691.CrossRefGoogle Scholar
[7]Pandit, S.G., “On the stability of impulsively perturbed differential systems”, Bull. Austral. Math. Soc. 17 (1977), 423–432.CrossRefGoogle Scholar
[8]Raghavendra, V. and Rao, M. Rama Mohana, “Integral equations of Volterra type and admissibility theory”, Rev. Roum. Math. Pure Appl. 18 (1973), 571–580.Google Scholar
[9]Raghavendra, V. and Rao, M. Rama Mohana, “Volterra integral equations with discontinuous perturbations”, Mathematica (Cluj) (to appear).Google Scholar
[10]Strauss, Aaron, “On a perturbed Volterra integral equation”, J. Math. Anal. Appl. 30 (1970), 564–575.Google Scholar