Published online by Cambridge University Press: 26 February 2009
Let q≥2 and N≥1 be integers. W. Zhang recently proved that for any fixed ε>0 and qε≤N≤q1/2−ε, 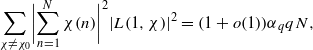 where the sum is taken over all nonprincipal characters χ modulo q, L(1,χ) denotes the L-functions corresponding to χ, and αq=qo(1) is some explicit function of q. Here we improve this result and show that the same asymptotic formula holds in the essentially full range qε≤N≤q1−ε.
where the sum is taken over all nonprincipal characters χ modulo q, L(1,χ) denotes the L-functions corresponding to χ, and αq=qo(1) is some explicit function of q. Here we improve this result and show that the same asymptotic formula holds in the essentially full range qε≤N≤q1−ε.
During the preparation of this work, the author was supported in part by ARC Grant DP0556431.