Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T20:08:46.618Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SOME PROPERTIES OF QUASI-DISTANCE-BALANCED GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  30 January 2018

ADEMIR HUJDUROVIĆ Open the ORCID record for ADEMIR HUJDUROVIĆ [Opens in a new window]
ADEMIR HUJDUROVIĆ*
Affiliation:
University of Primorska, FAMNIT, Glagoljaška 8, 6000 Koper, Slovenia University of Primorska, IAM, Muzejski trg 2, 6000 Koper, Slovenia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an edge 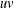$uv$ in a graph 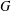$G$, 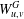$W_{u,v}^{G}$ denotes the set of all vertices of 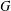$G$ that are closer to $u$ than to $v$. A graph 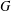$G$ is said to be quasi-distance-balanced if there exists a constant 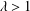$\unicode[STIX]{x1D706}>1$ such that 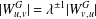$|W_{u,v}^{G}|=\unicode[STIX]{x1D706}^{\pm 1}|W_{v,u}^{G}|$ for every pair of adjacent vertices $u$ and $v$. The existence of nonbipartite quasi-distance-balanced graphs is an open problem. In this paper we investigate the possible structure of cycles in quasi-distance-balanced graphs and generalise the previously known result that every quasi-distance-balanced graph is triangle-free. We also prove that a connected quasi-distance-balanced graph admitting a bridge is isomorphic to a star. Several open problems are posed.

Keywords

distance-balanced graphsquasi-distance-balanced graphsbipartite graphsbridge

MSC classification

Primary: 05C12: Distance in graphs
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 177 - 184
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Abedi, A., Alaeiyan, M., Hujdurović, A. and Kutnar, K., ‘Quasi-𝜆-distance-balanced graphs’, Discrete Appl. Math. 227 (2017), 21–28.CrossRefGoogle Scholar
Balakrishnan, K., Changat, M., Peterin, I., Špacapan, S., Šparl, P. and Subhamathi, A. R., ‘Strongly distance-balanced graphs and graph products’, European J. Combin. 30 (2009), 1048–1053.CrossRefGoogle Scholar
Cabello, S. and Lukšič, P., ‘The complexity of obtaining a distance-balanced graph’, Electron. J. Combin. 18(1) (2011), Article ID #P49, 10 pages.Google Scholar
Djoković, D. Ž., ‘Distance-preserving subgraphs of hypercubes’, J. Combin. Theory Ser. B 14 (1973), 263–267.CrossRefGoogle Scholar
Gutman, I., ‘A formula for the Wiener number of trees and its extension to graphs containing cycles’, Graph Theory Notes N. Y. 27 (1994), 9–15.Google Scholar
Handa, K., ‘Bipartite graphs with balanced (a, b)-partitions’, Ars Combin. 51 (1999), 113–119.Google Scholar
Ilić, A., Klavžar, S. and Milanović, M., ‘On distance-balanced graphs’, European J. Combin. 31 (2010), 733–737.Google Scholar
Jerebic, J., Klavžar, S. and Rall, D. F., ‘Distance-balanced graphs’, Ann. Comb. 12 (2008), 71–79.CrossRefGoogle Scholar
Kutnar, K., Malnič, A., Marušič, D. and Miklavič, Š., ‘Distance-balanced graphs: symmetry conditions’, Discrete Math. 306 (2006), 1881–1894.CrossRefGoogle Scholar
Kutnar, K., Malnič, A., Marušič, D. and Miklavič, Š., ‘The strongly distance-balanced property of the generalized Petersen graphs’, Ars Math. Contemp. 2 (2009), 41–47.Google Scholar
Kutnar, K. and Miklavič, Š., ‘Nicely distance-balanced graphs’, European J. Combin. 39 (2014), 57–67.Google Scholar
Miklavič, Š. and Šparl, P., ‘On the connectivity of bipartite distance-balanced graphs’, European J. Combin. 33 (2012), 237–247.Google Scholar
Yang, R., Hou, X., Li, N. and Zhong, W., ‘A note on the distance-balanced property of generalized Petersen graphs’, Electron. J. Combin. 16(1) (2009), Article ID #N33, 3 pages.CrossRefGoogle Scholar