Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2025-01-03T17:54:40.787Z Has data issue: false hasContentIssue false
  • English
  • Français

On soluble groups of prime-power exponent

Published online by Cambridge University Press:  17 April 2009

Warren Brisley  and
L.G. Kovács
Warren Brisley
Affiliation:
University of Newcastle, Newcastle, New South Wales
L.G. Kovács
Affiliation:
Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be a prime and 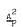the variety of elementary abelian by elementary abelian p-groups. A result of Brisley and Macdonald is generalized as follows. If H is a finite group in 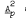and G is a soluble group of p–power exponent such that no section of G is isomorphic to H, then G is nilpotent and its class is bounded by a function of three variables: H, the exponent of G, and the soluble length of G. It is a corollary that if the variety generated by a soluble group G of finite exponent contains 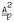, then each finite group in 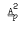is isomorphic to some section of G.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 4 , Issue 3 , June 1971 , pp. 389 - 396
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Brisley, Warren and Macdonald, I. D., “Two classes of metabelian p-groups”, Math. Z. 112 (1969), 5–12.CrossRefGoogle Scholar
[2]Gupta, N. D. and Newman, M. F., “On metabelian groups”, J. Austral. Math. Soc. 6 (1966), 362–368.CrossRefGoogle Scholar
[3]Hall, P., “Some sufficient conditions for a group to be nilpotent”, Illinois J. Math. 2 (1958), 787–801.CrossRefGoogle Scholar
[4]Higman, Graham, “Some remarks on varieties of groups”, Quart. J. Math. Oxford (2) 10 (1959), 105–178.CrossRefGoogle Scholar
[5]Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37, Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[6]Stewart, A. G. R., “On the class of certain nilpotent groups”, Proc. Roy. Soc. Ser. A 292 (1966), 374–379.Google Scholar