Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Easdown, D.
and
Munn, W.D.
1995.
Trace functions on inverse semigroup algebras.
Bulletin of the Australian Mathematical Society,
Vol. 52,
Issue. 3,
p.
359.
Crabb, M. J.
McGregor, C. M.
Munn, W. D.
and
Wassermann, S.
1996.
On the algebra of a free monoid.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 126,
Issue. 5,
p.
939.
Crabb, M. J.
and
Munn, W. D.
1998.
On the l1-algebra of certain monoids.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 128,
Issue. 5,
p.
1023.
Munn, W. D.
1998.
A note on special involutions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 65,
Issue. 2,
p.
284.
Munn, W. D.
2004.
Involutions on finite-dimensional algebras over real closed fields.
Journal of the Australian Mathematical Society,
Vol. 77,
Issue. 1,
p.
123.
Fountain, John
2010.
The work of Douglas Munn and its legacy.
Semigroup Forum,
Vol. 81,
Issue. 1,
p.
2.
Cheng, Herng Yi
and
Cheong, Kang Hao
2015.
Map composition generalized to coherent collections of maps.
Frontiers of Mathematics in China,
Vol. 10,
Issue. 3,
p.
547.
Kehayopulu, Niovi
2021.
On Involution Lattice Ordered Semigroups.
Lobachevskii Journal of Mathematics,
Vol. 42,
Issue. 1,
p.
124.
Bodor, Bertalan
Lehtonen, Erkko
Quinn-Gregson, Thomas
and
Verhulst, Nikolaas
2021.
HS-stability and complex products in involution semigroups.
Semigroup Forum,
Vol. 103,
Issue. 2,
p.
395.
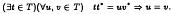 .
.