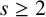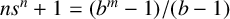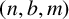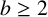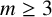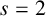1 Introduction
A Cullen number is a positive integer of the form
![]() $n2^n+1$
. Arithmetic properties of these numbers have been investigated in various papers. In 1976, Hooley [Reference Hooley2] showed that almost all Cullen numbers are composite. Luca and Stănică [Reference Luca, Stănică and Howard5] showed that there are only finitely many Fibonacci numbers among the Cullen numbers. More recently, Luca and Noubissie [Reference Luca and Noubissie4] showed that the largest prime factor of
$n2^n+1$
. Arithmetic properties of these numbers have been investigated in various papers. In 1976, Hooley [Reference Hooley2] showed that almost all Cullen numbers are composite. Luca and Stănică [Reference Luca, Stănică and Howard5] showed that there are only finitely many Fibonacci numbers among the Cullen numbers. More recently, Luca and Noubissie [Reference Luca and Noubissie4] showed that the largest prime factor of
![]() $n2^n+1\pm m!$
tends to infinity with
$n2^n+1\pm m!$
tends to infinity with
![]() $\max \{m,n\}$
and found all pairs
$\max \{m,n\}$
and found all pairs
![]() $(m,n)$
such that this number is of the form
$(m,n)$
such that this number is of the form
![]() $\pm 3^a\cdot 5^b\cdot 7^c$
for some nonnegative integers
$\pm 3^a\cdot 5^b\cdot 7^c$
for some nonnegative integers
![]() $a,b,c$
.
$a,b,c$
.
An s-Cullen number is a number of the form
![]() $ns^n+1$
where
$ns^n+1$
where
![]() $s\ge 2$
is a fixed integer. Grantham and Graves [Reference Grantham and Graves1] studied the Diophantine equation
$s\ge 2$
is a fixed integer. Grantham and Graves [Reference Grantham and Graves1] studied the Diophantine equation
and showed that under the
![]() $abc$
conjecture, it has only finitely many positive integer solutions
$abc$
conjecture, it has only finitely many positive integer solutions
![]() $(n,s,b,m)$
with
$(n,s,b,m)$
with
![]() $s\ge 2,~b\ge 2$
and
$s\ge 2,~b\ge 2$
and
![]() $m\ge 3$
. In this note, we assume that
$m\ge 3$
. In this note, we assume that
![]() $s\ge 2$
is fixed and prove that the equation (1.1) has only finitely many positive solutions in the remaining variables
$s\ge 2$
is fixed and prove that the equation (1.1) has only finitely many positive solutions in the remaining variables
![]() $(n,b,m)$
again with
$(n,b,m)$
again with
![]() $b\ge 2$
and
$b\ge 2$
and
![]() $m\ge 3$
. More precisely, we have the following result.
$m\ge 3$
. More precisely, we have the following result.
Theorem 1.1.
-
(i) For a fixed integer
 $s\ge 2$
, the Diophantine equation (1.1) has only finitely many positive integer solutions
$s\ge 2$
, the Diophantine equation (1.1) has only finitely many positive integer solutions
 $(n,b,m)$
with
$(n,b,m)$
with
 $b\ge 2$
and
$b\ge 2$
and
 $m\ge 3$
.
$m\ge 3$
. -
(ii) When
 $s=2$
, it has no solution.
$s=2$
, it has no solution.
2 The proof
We consider (i) and (ii) together. Let
![]() $s:=q_1^{\alpha _1} \cdots q_k^{\alpha _k}$
, where
$s:=q_1^{\alpha _1} \cdots q_k^{\alpha _k}$
, where
![]() $q_1,\ldots ,q_k$
are distinct primes and
$q_1,\ldots ,q_k$
are distinct primes and
![]() $\alpha _1,\ldots ,\alpha _k$
are positive integers. We expand the right-hand side and obtain
$\alpha _1,\ldots ,\alpha _k$
are positive integers. We expand the right-hand side and obtain
The proof proceeds in two cases.
Case 1.
![]() $\gcd (b,s)>1$
.
$\gcd (b,s)>1$
.
Assume that q is prime and
![]() $q\mid \gcd (s,b)$
. Letting
$q\mid \gcd (s,b)$
. Letting
![]() $\nu _q(\ell )$
denote the exponent of q in the factorisation of the nonzero integer
$\nu _q(\ell )$
denote the exponent of q in the factorisation of the nonzero integer
![]() $\ell $
, we see that
$\ell $
, we see that
![]() $\nu _q(ns^n)\ge n\nu _q(s)$
in the left-hand side of (2.1) whereas in the right-hand side of (2.1), we have
$\nu _q(ns^n)\ge n\nu _q(s)$
in the left-hand side of (2.1) whereas in the right-hand side of (2.1), we have
![]() $\nu _q(b^{m-1}+\cdots +b)=\nu _q(b)$
. Thus, if
$\nu _q(b^{m-1}+\cdots +b)=\nu _q(b)$
. Thus, if
![]() $q^{\alpha }\| s$
, then
$q^{\alpha }\| s$
, then
![]() $q^{n\alpha }\mid b$
. Let i be such that
$q^{n\alpha }\mid b$
. Let i be such that
![]() $q_1,\ldots ,q_i$
all divide b. If
$q_1,\ldots ,q_i$
all divide b. If
![]() $i=k$
, we then get that
$i=k$
, we then get that
![]() $s^n\mid b$
, so the right-hand side of (2.1) is at least
$s^n\mid b$
, so the right-hand side of (2.1) is at least
![]() $b^2>s^{2n}>ns^n$
, which is a contradiction. In particular, when
$b^2>s^{2n}>ns^n$
, which is a contradiction. In particular, when
![]() $s=2$
, Case 1 cannot occur. Next, take
$s=2$
, Case 1 cannot occur. Next, take
![]() $i<k$
. Write
$i<k$
. Write
![]() $s_1:=q_1^{\alpha _1}\cdots q_i^{\alpha _i}$
and put
$s_1:=q_1^{\alpha _1}\cdots q_i^{\alpha _i}$
and put
![]() $s_2:=s/s_1$
and
$s_2:=s/s_1$
and
![]() $b_1:=b/s_1^n$
. Then (2.1) can be rewritten as
$b_1:=b/s_1^n$
. Then (2.1) can be rewritten as
Cancelling
![]() $s_1^n$
, we get
$s_1^n$
, we get
and since
![]() $b_1$
and
$b_1$
and
![]() $s_2$
are coprime, it follows that
$s_2$
are coprime, it follows that
![]() $b_1\mid n$
. Thus,
$b_1\mid n$
. Thus,
or
The right-hand side is nonzero, since
![]() $m\ge 3$
, and
$m\ge 3$
, and
![]() $q_1^n\mid b$
. Applying a linear form in
$q_1^n\mid b$
. Applying a linear form in
![]() $q_1$
-adic logarithms to the left-hand side (which is nonzero since
$q_1$
-adic logarithms to the left-hand side (which is nonzero since
![]() $s_2\ge 2$
), we get
$s_2\ge 2$
), we get
where the constant implied by the
![]() $\ll $
symbol depends on s (in fact, it is of size
$\ll $
symbol depends on s (in fact, it is of size
![]() $O(q_1\log s_2)=O(s\log s)$
, where the constant implied by O is absolute). This gives a bound on n in this case.
$O(q_1\log s_2)=O(s\log s)$
, where the constant implied by O is absolute). This gives a bound on n in this case.
Case 2.
![]() $\gcd (b,s)=1$
.
$\gcd (b,s)=1$
.
Since (2.1) can be rewritten as
and s and b are coprime, we get
![]() $b\mid n$
. Thus,
$b\mid n$
. Thus,
In particular,
Since
![]() $b\mid n$
, it follows that
$b\mid n$
, it follows that
![]() $n^{m-1}\ge b^{m-1}>s^n\ge 2^n$
, and so
$n^{m-1}\ge b^{m-1}>s^n\ge 2^n$
, and so
![]() $m\gg n/{\log}\, n$
. However,
$m\gg n/{\log}\, n$
. However,
![]() $b^{m-1}<n^2s^n+1<s^{4n}$
, so
$b^{m-1}<n^2s^n+1<s^{4n}$
, so
![]() $m\ll n$
, where the constant implied by the last
$m\ll n$
, where the constant implied by the last
![]() $\ll $
symbol depends on s (it is in fact of size
$\ll $
symbol depends on s (it is in fact of size
![]() $O(\log s)$
where the constant implied by the O symbol is absolute). Next, we rewrite (2.2) as
$O(\log s)$
where the constant implied by the O symbol is absolute). Next, we rewrite (2.2) as
On the left-hand side (which is nonzero since the right-hand side is nonzero), we apply a linear form in logarithms á la Baker to get
 $$ \begin{align*} -(m-1)\log 2 & \ge -(m-1)\log b=\log|((b-1)(n/b)) b^{-m} s^n-1|\\[3pt] & \ge 0.5 |n\log s-m\log b+\log((b-1)(n/b)|\\[3pt] & \gg -(\log n)^2\log(\max\{m,n\})\\[3pt] & \gg -(\log n)^3, \end{align*} $$
$$ \begin{align*} -(m-1)\log 2 & \ge -(m-1)\log b=\log|((b-1)(n/b)) b^{-m} s^n-1|\\[3pt] & \ge 0.5 |n\log s-m\log b+\log((b-1)(n/b)|\\[3pt] & \gg -(\log n)^2\log(\max\{m,n\})\\[3pt] & \gg -(\log n)^3, \end{align*} $$
where the constant implied by the
![]() $\ll $
symbol can be taken to be
$\ll $
symbol can be taken to be
and the constant implied by O is absolute. Hence,
giving
![]() $n\ll (\log n)^4$
, so n is bounded. This finishes the proof of (i).
$n\ll (\log n)^4$
, so n is bounded. This finishes the proof of (i).
For (ii), when
![]() $s=2$
, only Case 2 is possible so b is odd and the left-hand side of (2.1) is even. Hence,
$s=2$
, only Case 2 is possible so b is odd and the left-hand side of (2.1) is even. Hence,
![]() $(b^{m-1}-1)/(b-1)$
is even and b is odd showing that
$(b^{m-1}-1)/(b-1)$
is even and b is odd showing that
![]() $m-1$
is even. Thus, (2.2) gives
$m-1$
is even. Thus, (2.2) gives
Thus,
![]() $(X,Y):=(b^{(m-1)/2},2^{\lfloor n/2\rfloor })$
satisfy
$(X,Y):=(b^{(m-1)/2},2^{\lfloor n/2\rfloor })$
satisfy
Thus,
![]() $(X,Y)=(X_k,Y_k)$
is the kth solution of the Pell equation (2.3). Since Y is a power of
$(X,Y)=(X_k,Y_k)$
is the kth solution of the Pell equation (2.3). Since Y is a power of
![]() $2$
, by the existence of primitive divisors for Lucas sequences, the only possibilities are
$2$
, by the existence of primitive divisors for Lucas sequences, the only possibilities are
![]() $k\in \{1,2\}$
. Thus,
$k\in \{1,2\}$
. Thus,
where the last inequality follows from Lemma 1 in [Reference Křížek and Luca3]. Since
![]() $d\le 2(b-1)(n/b)<2n$
, we get
$d\le 2(b-1)(n/b)<2n$
, we get
giving
![]() $n<10^5$
. To reduce it, we played around with Mathematica. If
$n<10^5$
. To reduce it, we played around with Mathematica. If
![]() $m\le 8$
, then since
$m\le 8$
, then since
![]() $b\mid n$
, we get
$b\mid n$
, we get
which gives
![]() $n\le 29$
. If
$n\le 29$
. If
![]() $m\ge 9$
, then
$m\ge 9$
, then
![]() $n2^n\equiv b+b^2+b^3+\cdots +b^7\pmod {b^8}$
. For each
$n2^n\equiv b+b^2+b^3+\cdots +b^7\pmod {b^8}$
. For each
![]() $n<10^5$
, we generated all odd divisors
$n<10^5$
, we generated all odd divisors
![]() $b>1$
of n and checked whether the above congruence held, and if it did, we recorded the value of b. The only b found was
$b>1$
of n and checked whether the above congruence held, and if it did, we recorded the value of b. The only b found was
![]() $b=3$
. Since
$b=3$
. Since
![]() $n2^n=(3^m-1)/2\ge (3^{9}-1)/2$
, we get
$n2^n=(3^m-1)/2\ge (3^{9}-1)/2$
, we get
![]() $n\ge 10$
. If
$n\ge 10$
. If
![]() $m-1\ge n$
, we then get
$m-1\ge n$
, we then get
![]() $n2^n=3^{m-1}+\cdots +1>3^n$
, which is a contradiction for
$n2^n=3^{m-1}+\cdots +1>3^n$
, which is a contradiction for
![]() $n\ge 10$
. Thus,
$n\ge 10$
. Thus,
so
![]() $2^{n+1}\mid 3^{m-1}-1$
. This implies that
$2^{n+1}\mid 3^{m-1}-1$
. This implies that
![]() $m-1$
is even and further, calculating the exponent of
$m-1$
is even and further, calculating the exponent of
![]() $2$
in
$2$
in
![]() $3^{m-1}-1$
, we get
$3^{m-1}-1$
, we get
 $$ \begin{align*} n+1 & \le \nu_2(3^{m-1}-1)=3+\nu_2((m-1)/2)\\[2pt] & < 3+(\log(n/2))/{\log}\, 2=2+(\log n)/{\log}\, 2\\[2pt] & < 1.5\log n+2, \end{align*} $$
$$ \begin{align*} n+1 & \le \nu_2(3^{m-1}-1)=3+\nu_2((m-1)/2)\\[2pt] & < 3+(\log(n/2))/{\log}\, 2=2+(\log n)/{\log}\, 2\\[2pt] & < 1.5\log n+2, \end{align*} $$
which is false for
![]() $n\ge 10$
. This shows that
$n\ge 10$
. This shows that
![]() $m\ge 9$
is not possible, and so only
$m\ge 9$
is not possible, and so only
![]() $m\le 8$
is possible for which we already saw that
$m\le 8$
is possible for which we already saw that
![]() $n\le 29$
. Finally, we took all
$n\le 29$
. Finally, we took all
![]() $n\in [2,29]$
, found all odd divisors
$n\in [2,29]$
, found all odd divisors
![]() $b>1$
of n (if any), calculated the potential m using the equation
$b>1$
of n (if any), calculated the potential m using the equation
![]() $m-1:= \lfloor \log (n2^n+1)/{\log}\, b\rfloor $
and checked whether (1.1) holds with
$m-1:= \lfloor \log (n2^n+1)/{\log}\, b\rfloor $
and checked whether (1.1) holds with
![]() $s=2$
. No solution was found.
$s=2$
. No solution was found.
This finishes the proof.
3 Comments
Closely related to Cullen numbers are the Woodall numbers of the form
![]() $n2^n-1$
or, more generally,
$n2^n-1$
or, more generally,
![]() $ns^n-1$
with some
$ns^n-1$
with some
![]() $s\ge 2$
. Our argument does not extend to Woodall numbers so we leave the topic of exploring the analogous Diophantine equation (1.1) with Cullen numbers replaced by Woodall numbers to the interested reader.
$s\ge 2$
. Our argument does not extend to Woodall numbers so we leave the topic of exploring the analogous Diophantine equation (1.1) with Cullen numbers replaced by Woodall numbers to the interested reader.