Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T00:44:13.518Z Has data issue: false hasContentIssue false
  • English
  • Français

ON REAL PARTS OF POWERS OF COMPLEX PISOT NUMBERS

Part of: Diophantine approximation, transcendental number theory Algebraic number theory: global fields

Published online by Cambridge University Press:  16 March 2016

TOUFIK ZAÏMI
TOUFIK ZAÏMI*
Affiliation:
Department of Mathematics and Statistics, College of Science, Al Imam Mohammad Ibn Saud Islamic University, PO Box 90950, Riyadh 11623, Saudi Arabia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that a nonreal algebraic number 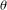$\unicode[STIX]{x1D703}$ with modulus greater than 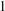$1$ is a complex Pisot number if and only if there is a nonzero complex number $\unicode[STIX]{x1D706}$ such that the sequence of fractional parts 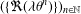$(\{\Re (\unicode[STIX]{x1D706}\unicode[STIX]{x1D703}^{n})\})_{n\in \mathbb{N}}$ has a finite number of limit points. Also, we characterise those complex Pisot numbers 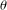$\unicode[STIX]{x1D703}$ for which there is a convergent sequence of the form 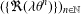$(\{\Re (\unicode[STIX]{x1D706}\unicode[STIX]{x1D703}^{n})\})_{n\in \mathbb{N}}$ for some 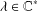$\unicode[STIX]{x1D706}\in \mathbb{C}^{\ast }$. These results are generalisations of the corresponding real ones, due to Pisot, Vijayaraghavan and Dubickas.

Keywords

complex Pisot numbersdistribution modulo one

MSC classification

Primary: 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure
Secondary: 11J71: Distribution modulo one 11R80: Totally real fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 245 - 253
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Batut, C., Bernardi, D., Cohen, H. and Olivier, M., ‘User’s guide to PARI-GP’, ver. 2.5.1, Université Bordeaux 1, 2012. pari.math.u-bordeaux.fr/pub/pari/manuals/2.5.1/users.pdf.Google Scholar
Bertin, M. J., Decomps-Guilloux, A., Grandet-Hugo, M., Pathiaux-Delefosse, M. and Schreiber, J. P., Pisot and Salem Numbers (Birkhäuser, Basel, 1992).CrossRefGoogle Scholar
Bertin, M. J. and Zaïmi, T., ‘Complex Pisot numbers in algebraic number fields’, C. R. Math. Acad. Sci. Paris 353 (2015), 965–967.Google Scholar
Boyd, D. W., ‘Linear recurrence relations for some generalized Pisot sequences’, in: Advances in Number Theory, Proc. Third Conf. Canadian Number Theory Association, 1991 (Oxford University Press, Oxford, 1993), 333–340.Google Scholar
Boyd, D. W., ‘Irreducible polynomials with many roots of maximal modulus’, Acta Arith. 68 (1994), 85–88.Google Scholar
Bugeaud, Y., An Introduction to Diophantine Approximation (Cambridge University Press, Cambridge, 2012).Google Scholar
Cantor, D. G., ‘On sets of algebraic integers whose remaining conjugates lie in the unit circle’, Trans. Amer. Math. Soc. 105 (1962), 391–406.Google Scholar
Chamfy, C., ‘Fonctions méromorphes dans le cercle-unité et leurs séries de Taylor’, Ann. Inst. Fourier (Grenoble) 8 (1958), 211–251.Google Scholar
Dubickas, A., ‘Integer parts of powers of Pisot and Salem numbers’, Arch. Math. (Basel) 79 (2002), 252–257.Google Scholar
Dubickas, A., ‘On the limit points of the fractional parts of powers of Pisot numbers’, Arch. Math. (Brno) 42 (2006), 151–158.Google Scholar
Dufresnoy, J. and Pisot, C., ‘Sur un ensemble fermé d’entiers algébriques’, Ann. Sci. Éc. Norm. Supér. (4) 70 (1953), 105–133.Google Scholar
Dufresnoy, J. and Pisot, C., ‘Étude de certaines fonctions méromorphes bornées sur le cercle unité, application à un ensemble fermé d’entiers algébriques’, Ann. Sci. Éc. Norm. Supér. (4) 72 (1955), 69–72.CrossRefGoogle Scholar
Ferguson, R., ‘Irreducible polynomials with many roots of equal modulus’, Acta Arith. 78 (1997), 221–225.Google Scholar
Garth, D., ‘Complex Pisot numbers of small modulus’, C. R. Math. Acad. Sci. Paris 336 (2003), 967–970.CrossRefGoogle Scholar
Kelly, J. B., ‘A closed set of algebraic integers’, Amer. J. Math. 72 (1950), 565–572.Google Scholar
Pisot, C., ‘Répartition (mod 1) des puissances successives des nombres réels’, Comment. Math. Helv. 19 (1946), 153–160.Google Scholar
Salem, R., ‘A remarkable class of integers. Proof of a conjecture of Vijayaraghavan’, Duke Math. J. 11 (1944), 103–108.Google Scholar
Samet, P. A., ‘Algebraic integers with two conjugates outside the unit circle’, Math. Proc. Cambridge Philos. Soc. 49 (1953), 421–436.CrossRefGoogle Scholar
Smyth, C. J., ‘The conjugates of algebraic integers’, Amer. Math. Monthly 82 (1975), 86.Google Scholar
Vijayaraghavan, T., ‘On the fractional parts of the powers of a number. II’, Math. Proc. Cambridge Philos. Soc. 37 (1941), 349–357.Google Scholar
Zaïmi, T., ‘An arithmetical property of powers of Salem numbers’, J. Number Theory 120 (2006), 179–191.Google Scholar
Zaïmi, T., ‘On integer and fractional parts of powers of Salem numbers’, Arch. Math. 87 (2006), 124–128.Google Scholar
Zaïmi, T., ‘Comments on the distribution modulo one of powers of Pisot and Salem numbers’, Publ. Math. Debrecen 80 (2012), 417–426.CrossRefGoogle Scholar
Zaïmi, T., ‘On the conjugates of certain algebraic integers’, Publications de l’Institut Mathématiques, to appear.Google Scholar
Zaïmi, T., Selatnia, M. and Zekraoui, H., ‘Comments on the fractional parts of Pisot numbers’, Arch. Math. (Brno) 51 (2015), 153–161.CrossRefGoogle Scholar