Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T02:33:02.881Z Has data issue: false hasContentIssue false
  • English
  • Français

On rational approximations of the exponential function at rational points

Published online by Cambridge University Press:  17 April 2009

Kurt Mahler
Kurt Mahler
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p, q, u, and v be any four positive integers, and let further δ be a number in the interval 0 < δ ≤ 2. In this note an effective lower bound for q will be obtained which insures that 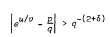In the special case when u = v = 1, it was shown by J. Popken, Math. Z. 29 (1929), 525–541, that 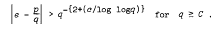Here c and C are two positive absolute constants which, however, were not determined explicity. A similarly non-effective result was given in my paper, J. reine angew. Math. 166 (1932), 118–150.

The method of this note depends again on the classical formulae by Hermite which I applied also op. cit.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 10 , Issue 3 , June 1974 , pp. 325 - 335
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Mahler, Kurt, “Zur Approximation der Exponentialfunktion und des Logarithmus, Teil I”, J. Reine angew. Math. 166 (1932), 118–136 (1931).CrossRefGoogle Scholar
[2]Mahler, Kurt, “Zur Approximation der Exponentialfunktion und des Logarithmus, Teil II”, J. reine angew. Math. 166 (1932), 137–150.CrossRefGoogle Scholar
[3]Popken, J., “Zur Transzendenz von e”, Math. Z. 29 (1929), 525–541.CrossRefGoogle Scholar