Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T12:02:12.475Z Has data issue: false hasContentIssue false
  • English
  • Français

ON QUANTITATIVE SCHUR AND DUNFORD–PETTIS PROPERTIES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  26 February 2015

ONDŘEJ F. K. KALENDA  and
JIŘÍ SPURNÝ
ONDŘEJ F. K. KALENDA
Affiliation:
Department of Mathematical Analysis, Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 186 75, Praha 8, Czech Republic email [email protected]
JIŘÍ SPURNÝ*
Affiliation:
Department of Mathematical Analysis, Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 186 75, Praha 8, Czech Republic email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the dual to any subspace of 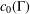$c_{0}({\rm\Gamma})$ (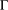${\rm\Gamma}$ is an arbitrary index set) has the strongest possible quantitative version of the Schur property. Further, we establish a relationship between the quantitative Schur property and quantitative versions of the Dunford–Pettis property. Finally, we apply these results to show, in particular, that any subspace of the space of compact operators on 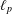$\ell _{p}$ (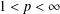$1<p<\infty$) with the Dunford–Pettis property automatically satisfies both its quantitative versions.

Keywords

quantitative Schur propertyquantitative Dunford–Pettis property

MSC classification

Primary: 46B25: Classical Banach spaces in the general theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 3 , June 2015 , pp. 471 - 486
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bourgain, J. and Delbaen, F., ‘A class of special L∞ spaces’, Acta Math. 145(3–4) (1980), 155–176.Google Scholar
Brown, S. W., ‘Weak sequential convergence in the dual of an algebra of compact operators’, J. Operator Theory 33(1) (1995), 33–42.Google Scholar
Cembranos, P., ‘The hereditary Dunford–Pettis property on C (K, E)’, Illinois J. Math. 31(3) (1987), 365–373.Google Scholar
Diestel, J., ‘A survey of results related to the Dunford–Pettis property’, in: Proceedings of the Conference on Integration, Topology, and Geometry in Linear Spaces (Univ. North Carolina, Chapel Hill, NC, 1979 (Providence, RI, 1980), Contemporary Mathematics, 2 (American Mathematical Society, Providence, RI) 15–60.Google Scholar
Freeman, D., Odell, E. and Schlumprecht, T., ‘The universality of ℓ 1 as a dual space’, Math. Ann. 351(1) (2011), 149–186.CrossRefGoogle Scholar
Hagler, J., ‘A counterexample to several questions about Banach spaces’, Studia Math. 60(3) (1977), 289–308.Google Scholar
Haydon, R., ‘Subspaces of the Bourgain–Delbaen space’, Studia Math. 139(3) (2000), 275–293.Google Scholar
Kačena, M., Kalenda, O. F. and Spurný, J., ‘Quantitative Dunford–Pettis property’, Adv. Math. 234 (2013), 488–527.Google Scholar
Kalenda, O. F. K., Pfitzner, H. and Spurný, J., ‘On quantification of weak sequential completeness’, J. Funct. Anal. 260(10) (2011), 2986–2996.CrossRefGoogle Scholar
Kalenda, O. F. K. and Spurný, J., ‘On a difference between quantitative weak sequential completeness and the quantitative Schur property’, Proc. Amer. Math. Soc. 140(10) (2012), 3435–3444.CrossRefGoogle Scholar
Kalton, N. J. and Werner, D., ‘Property (M), M-ideals, and almost isometric structure of Banach spaces’, J. reine angew. Math. 461 (1995), 137–178.Google Scholar
Pełczyński, A., ‘On Banach spaces containing L 1(𝜇)’, Studia Math. 30 (1968), 231–246.Google Scholar
Pełczyński, A. and Szlenk, W., ‘An example of a non-shrinking basis’, Rev. Roumaine Math. Pures Appl. 10 (1965), 961–966.Google Scholar
Saksman, E. and Tylli, H.-O., ‘Structure of subspaces of the compact operators having the Dunford–Pettis property’, Math. Z. 232 (1999), 411–425.Google Scholar