Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T10:38:36.818Z Has data issue: false hasContentIssue false
  • English
  • Français

On p–valent starlike functions with reference to the Bernardi integral operator

Published online by Cambridge University Press:  17 April 2009

Vinod Kumar  and
S.L. Shukla
Vinod Kumar
Affiliation:
Dr V. Kumar, Department of Mathematics, Christ Church College, Kanpur–208001, India.
S.L. Shukla
Affiliation:
Dr S.L. Shukla, Department of Mathematics, Janta College, Bakewar, Etawah–206124, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 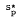(A, B) denote the class of certain p-valent starlike functions. Recently G. Lakshma Reddy and K.S. Padmanabhan [Bull. Austral. Math. Soc. 25 (1982), 387–396] have shown that the function g defined by

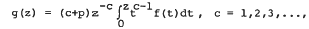
belongs to the class 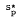(A, B) if f ∈ 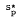(A, B). The technique used by them fails when c is any positive real number. In this paper, by employing a more powerful technique, we improve their result to the case when c is any real number such that c ≥ −p(1+A)/(1+B).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 30 , Issue 1 , August 1984 , pp. 37 - 43
Copyright
Copyright © Australian Mathematical Society 1984

References

[1;]Bernardi, S.D., “Convex and starlike univalent functions”, Trans. Amer. Math. Soc. 135 (1969), 429–446.CrossRefGoogle Scholar
[2]Gupta, Ved P. and Jain, Pawan K., “On starlike functions”, Rend. Mat. 9 (1976), 433–437.Google Scholar
[3]Jack, I.S., “Functions starlike and convex of order α”, J. London Math. Soc. (2) 3 (1971), 469–474.Google Scholar
[4]Kumar, Vinod and Shukla, S.L., “Bazilevič integral operators”, Rend. Mat. 3 (1983).Google Scholar
[5]Miller, Sanford S., Mocanu, Petru T. and Reade, Maxwell O., “Starlike integral operators”, Pacific J. Math. 79 (1978), 157–168.CrossRefGoogle Scholar
[6]Reddy, G. Lakshma and Padmanabhan, K.S., “On analytic functions with reference to Bernardi integral operator”. Bull. Austral. Math. Soc. 25 (1982), 387–396.Google Scholar