No CrossRef data available.
Published online by Cambridge University Press: 27 July 2023
Assume that G is a finite group, N is a nontrivial normal subgroup of G and p is an odd prime. Let 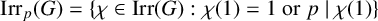 $\mathrm{Irr}_p(G)=\{\chi \in \mathrm{Irr}(G) : \chi (1)=1~\mathrm{or}~ p \mid \chi (1)\}$ and
$\mathrm{Irr}_p(G)=\{\chi \in \mathrm{Irr}(G) : \chi (1)=1~\mathrm{or}~ p \mid \chi (1)\}$ and 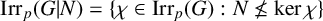 $\mathrm{Irr}_p(G|N)=\{\chi \in \mathrm{Irr}_p(G) : N \not \leq \mathrm{ker}\,\chi \}$. The average character degree of irreducible characters of
$\mathrm{Irr}_p(G|N)=\{\chi \in \mathrm{Irr}_p(G) : N \not \leq \mathrm{ker}\,\chi \}$. The average character degree of irreducible characters of 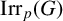 $\mathrm{Irr}_p(G)$ and the average character degree of irreducible characters of
$\mathrm{Irr}_p(G)$ and the average character degree of irreducible characters of 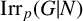 $\mathrm{Irr}_p(G|N)$ are denoted by
$\mathrm{Irr}_p(G|N)$ are denoted by 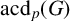 $\mathrm{acd}_p(G)$ and
$\mathrm{acd}_p(G)$ and 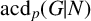 $\mathrm{acd}_p(G|N)$, respectively. We show that if
$\mathrm{acd}_p(G|N)$, respectively. We show that if 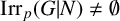 $\mathrm{Irr}_p(G|N) \neq \emptyset $ and
$\mathrm{Irr}_p(G|N) \neq \emptyset $ and 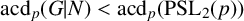 $\mathrm{acd}_p(G|N) < \mathrm{acd}_p(\mathrm{PSL}_2(p))$, then G is p-solvable and
$\mathrm{acd}_p(G|N) < \mathrm{acd}_p(\mathrm{PSL}_2(p))$, then G is p-solvable and 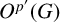 $O^{p'}(G)$ is solvable. We find examples that make this bound best possible. Moreover, we see that if
$O^{p'}(G)$ is solvable. We find examples that make this bound best possible. Moreover, we see that if 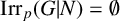 $\mathrm{Irr}_p(G|N) = \emptyset $, then N is p-solvable and
$\mathrm{Irr}_p(G|N) = \emptyset $, then N is p-solvable and 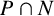 $P \cap N$ and
$P \cap N$ and 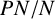 $PN/N$ are abelian for every
$PN/N$ are abelian for every 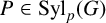 $P \in \mathrm{Syl}_p(G)$.
$P \in \mathrm{Syl}_p(G)$.