No CrossRef data available.
Article contents
ON PSEUDO-NULLITY OF THE FINE MORDELL–WEIL GROUP
Published online by Cambridge University Press: 03 February 2025
Abstract
Let E be an elliptic curve defined over  $\mathbb {Q}$ with good ordinary reduction at a prime
$\mathbb {Q}$ with good ordinary reduction at a prime 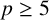 $p\geq 5$ and let F be an imaginary quadratic field. Under appropriate assumptions, we show that the Pontryagin dual of the fine Mordell–Weil group of E over the
$p\geq 5$ and let F be an imaginary quadratic field. Under appropriate assumptions, we show that the Pontryagin dual of the fine Mordell–Weil group of E over the 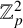 $\mathbb {Z}_{p}^2$-extension of F is pseudo-null as a module over the Iwasawa algebra of the group
$\mathbb {Z}_{p}^2$-extension of F is pseudo-null as a module over the Iwasawa algebra of the group 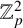 $\mathbb {Z}_{p}^2$.
$\mathbb {Z}_{p}^2$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Chao Qin’s research is supported by the National Natural Science Foundation of China under Grant No. 12001546, Heilongjiang Province under Grant No. 3236330122 and Harbin Engineering University under Grant No. GK0000020127. Jun Wang’s research is supported by the National Natural Science Foundation of China under Grant No. 12331004.



