Hostname: page-component-6bf8c574d5-k2jvg Total loading time: 0 Render date: 2025-03-08T01:36:27.600Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PARTITIONS OF NONNEGATIVE INTEGERS AND REPRESENTATION FUNCTIONS

Part of: Sequences and sets

Published online by Cambridge University Press:  11 December 2018

XIAO-HUI YAN Open the ORCID record for XIAO-HUI YAN [Opens in a new window]
XIAO-HUI YAN*
Affiliation:
School of Mathematical Sciences and Institute of Mathematics, Nanjing Normal University, Nanjing 210023, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 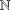$\mathbb{N}$ be the set of all nonnegative integers. For any set 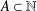$A\subset \mathbb{N}$, let 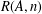$R(A,n)$ denote the number of representations of $n$ as 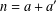$n=a+a^{\prime }$ with 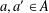$a,a^{\prime }\in A$. There is no partition 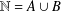$\mathbb{N}=A\cup B$ such that 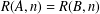$R(A,n)=R(B,n)$ for all sufficiently large integers $n$. We prove that a partition 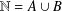$\mathbb{N}=A\cup B$ satisfies 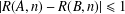$|R(A,n)-R(B,n)|\leq 1$ for all nonnegative integers $n$ if and only if, for each nonnegative integer 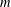$m$, exactly one of 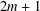$2m+1$ and 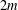$2m$ is in 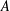$A$.

Keywords

representation functionpartitionSárközy problem

MSC classification

Primary: 11B34: Representation functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 385 - 387
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The author is supported by the National Natural Science Foundation of China, Grant No. 11771211.

References

Chen, Y.-G. and Wang, B., ‘On additive properties of two special sequences’, Acta Arith. 110 (2003), 299–303.Google Scholar
Dombi, G., ‘Additive properties of certain sets’, Acta Arith. 103 (2002), 137–146.Google Scholar
Kiss, S. Z. and Sándor, C., ‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161.Google Scholar
Li, J.-W. and Tang, M., ‘Partitions of the set of nonnegative integers with the same representation functions’, Bull. Aust. Math. Soc. 97 (2018), 200–206.Google Scholar
Tang, M. and Chen, S.-Q., ‘On a problem of partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 341 (2018), 3075–3078.Google Scholar
Tang, M. and Li, J.-W., ‘On the structure of some sets which have the same representation functions’, Period. Math. Hungar. doi:10.1007/s10998-018-0240-5.Google Scholar